Question

In the given figure BO and CO are respectively the bisectors of $\angle B$ and $\angle C$ of $\Delta ABC$. AO produced meets BC at P.

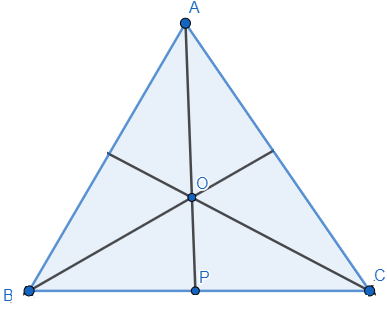
Show that
(i) $\dfrac{AB}{BP}=\dfrac{AO}{OP}$
(ii) $\dfrac{AC}{CP}=\dfrac{AO}{OP}$
(iii) $\dfrac{AB}{AC}=\dfrac{BP}{PC}$
(iv) AP is the bisector of $\angle BAC$

Answer 1

Hint: We use the angle bisector formula to get the first two solutions using the relation only. We use those two proved relations to find the third proof. After getting the third proved, we use that with the help of the inverse of the angle bisector theorem to get to the fourth prove.

Complete step by step answer:
We are going to use the angle bisector theorem of triangles.
The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
In the figure, BO and CO are respectively the bisectors of $\angle B$ and $\angle C$ of $\Delta ABC$.
So, $\angle ABO=\angle CBO=\dfrac{1}{2}\angle ABC$, $\angle ACO=\angle BCO=\dfrac{1}{2}\angle ACB$.
In $\Delta ABP$, BO acts as the bisector.
So, $\dfrac{AB}{BP}=\dfrac{AO}{OP}$ … (1) [$\because \angle ABO=\angle CBO$]
Now we take $\Delta ABP$ where CO acts as a bisector.
It gives $\dfrac{AC}{CP}=\dfrac{AO}{OP}$ …(2) [$\because \angle ACO=\angle BCO$]
From equation (1) and (2) we get $\dfrac{AB}{BP}=\dfrac{AO}{OP}=\dfrac{AC}{CP}$ which gives us $\dfrac{AB}{BP}=\dfrac{AC}{CP}$.
We cross-change to get $\dfrac{AB}{AC}=\dfrac{BP}{PC}$.
The inverse of the angle-bisector theorem is also true.
Now in case of $\Delta ABC$ we got $\dfrac{AB}{AC}=\dfrac{BP}{PC}$. So, $\angle BAP=\angle CAP$.
It gives us AP is the angle bisector of $\angle BAC$.

Note: In the theorem, we need to remember that the relationship is with the relative lengths of the other two sides of the triangle. We can’t confuse it with the theorem of a similar triangle or the congruent triangle.