
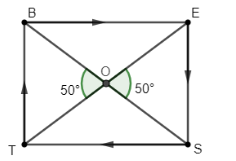
In the given figure, BEST is a rectangle in which diagonals BS and TE intersect at O. If $\angle EOS=50{}^\circ $, then $\angle OBT$
(a) $56{}^\circ $
(b) $45{}^\circ $
(c) $65{}^\circ $
(d) None of these

Answer
602.7k+ views
Hint: First, as we know that diagonals of rectangles are bisecting means diagonals are divided into equal length so, $BO=OS=EO=OT$ will be equal. Then, the sum of angles of the triangle $180{}^\circ $ using this angle OBT can be found.
Complete step-by-step answer:
In the question, we are given a rectangle whose diagonals bisect each other. Also, $\angle EOS=50{}^\circ $ and $\angle BOT=50{}^\circ $ is given. So, the diagram is as shown below.
Here, we will use the theorem which stated that “diagonals of a rectangle are equal”. This means that the length of ET and BS are equal. So, O is the intersection point which intersects both the diagonals.
So, Diagonals are bisecting here which means dividing into two parts which will be equal. Therefore, $BO=OS=EO=OT$ are equal in length.
(Dotted line shown means it is having same length)
Now, we have to find $\angle OBT$ , So we know that summation of angles of triangle is equal to $180{}^\circ $ . So, we get
$180{}^\circ =\angle BOT+\angle OTB+\angle OBT$ …………………..(1)
Now, as we know OT and OB are equal in length it means $\Delta BOT$ is an isosceles triangle and also the opposite angle of side OT and OB are equal. Thus, we get
$\Rightarrow \angle OTB=\angle OBT$
So, substituting the above value in equation (1) we get,
$180{}^\circ =\angle BOT+\angle OBT+\angle OBT=\angle BOT+2\angle OBT$
We know that $\angle BOT=50{}^\circ $ is given, so we get
\[180{}^\circ =50{}^\circ +2\angle OBT\]
\[180{}^\circ -50{}^\circ =2\angle OBT\]
\[\dfrac{130{}^\circ }{2}=65{}^\circ =\angle OBT\]
Thus, \[\angle OBT=65{}^\circ \] .
Option (c) is the correct answer.
Note: Be careful in this type of problem because students generally consider that all the angles of rectangle are \[90{}^\circ \] i.e. right angle so, as diagonals are bisecting means angles also bisect in two part which means \[\dfrac{90{}^\circ }{2}=45{}^\circ \] . Thus, \[\angle OBT=45{}^\circ \] which is a completely wrong answer. So, don’t make this mistake. Also, if students apply this method then they must verify by adding 3 angles of triangle whether their sum is \[180{}^\circ \]or not. So, this way also mistakes can be avoided by verification.
Complete step-by-step answer:
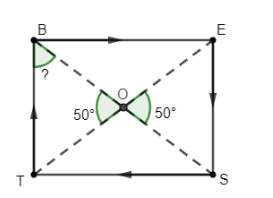
In the question, we are given a rectangle whose diagonals bisect each other. Also, $\angle EOS=50{}^\circ $ and $\angle BOT=50{}^\circ $ is given. So, the diagram is as shown below.

Here, we will use the theorem which stated that “diagonals of a rectangle are equal”. This means that the length of ET and BS are equal. So, O is the intersection point which intersects both the diagonals.
So, Diagonals are bisecting here which means dividing into two parts which will be equal. Therefore, $BO=OS=EO=OT$ are equal in length.
(Dotted line shown means it is having same length)
Now, we have to find $\angle OBT$ , So we know that summation of angles of triangle is equal to $180{}^\circ $ . So, we get
$180{}^\circ =\angle BOT+\angle OTB+\angle OBT$ …………………..(1)
Now, as we know OT and OB are equal in length it means $\Delta BOT$ is an isosceles triangle and also the opposite angle of side OT and OB are equal. Thus, we get
$\Rightarrow \angle OTB=\angle OBT$
So, substituting the above value in equation (1) we get,
$180{}^\circ =\angle BOT+\angle OBT+\angle OBT=\angle BOT+2\angle OBT$
We know that $\angle BOT=50{}^\circ $ is given, so we get
\[180{}^\circ =50{}^\circ +2\angle OBT\]
\[180{}^\circ -50{}^\circ =2\angle OBT\]
\[\dfrac{130{}^\circ }{2}=65{}^\circ =\angle OBT\]
Thus, \[\angle OBT=65{}^\circ \] .
Option (c) is the correct answer.
Note: Be careful in this type of problem because students generally consider that all the angles of rectangle are \[90{}^\circ \] i.e. right angle so, as diagonals are bisecting means angles also bisect in two part which means \[\dfrac{90{}^\circ }{2}=45{}^\circ \] . Thus, \[\angle OBT=45{}^\circ \] which is a completely wrong answer. So, don’t make this mistake. Also, if students apply this method then they must verify by adding 3 angles of triangle whether their sum is \[180{}^\circ \]or not. So, this way also mistakes can be avoided by verification.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Who is eligible for RTE class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




