Question

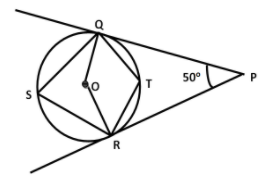
In the given figure below, $\angle QSR$ is equal to

A) ${{65}^{\circ }}$
B) ${{50}^{\circ }}$
C) ${{70}^{\circ }}$
D) ${{75}^{\circ }}$

Answer 1

Hint: Here we will first consider the quadrilateral whose one angle is given. We know that the radius of a circle makes a right angle to the tangent. From there, we will get the other two angles of the quadrilateral. Then we will find the fourth angle of the quadrilateral using the property of quadrilateral. Then we will find the required angle by using the property of an arc which states that the angle made by an arc at the center is equal to two times the angle made by the same arc at the circumference of the circle.

Complete step by step solution:
We know that the angle between the radius and tangent to the circle is ${{90}^{\circ }}$.
Therefore, $\angle OQP=\angle ORP={{90}^{\circ }}$
In quadrilateral $OQPR$, we have
$\begin{align}
  & \angle OQP=\angle ORP={{90}^{\circ }} \\
 & \angle QPR={{50}^{\circ }} \\
\end{align}$
Now, we will find $\angle QOR$ of quadrilateral $OQPR$. We know that the sum of angles of a quadrilateral is equal to ${{360}^{\circ }}$.
Applying this property in quadrilateral $OQPR$, we get
$\Rightarrow \angle OQP+\angle ORP+\angle QPR+\angle QOR={{360}^{\circ }}$
Now, we will substitute the value of known values of all three angles of a quadrilateral $OQPR$.
$\Rightarrow {{90}^{\circ }}+{{90}^{\circ }}+{{50}^{\circ }}+\angle QOR={{360}^{\circ }}$
Adding all the terms on left side, we get
$\Rightarrow {{230}^{\circ }}+\angle QOR={{360}^{\circ }}$
Now, we will subtract ${{230}^{\circ }}$ from both sides.
$\Rightarrow {{230}^{\circ }}-{{230}^{\circ }}+\angle QOR={{360}^{\circ }}-{{230}^{\circ }}$
On subtracting the terms on both sides, we get
$\Rightarrow \angle QOR={{130}^{\circ }}$
We know one property of an arc which states that the angle made by an arc at the center is equal to two times the angle made by the same arc at the circumference of the circle.
Using this property for an arc $QTR$, we get
b$\Rightarrow \angle QOR=2\angle QSR$
Now, we will substitute the value of angle $QOR$, we get
$\Rightarrow {{130}^{\circ }}=2\angle QSR$
Dividing both sides by 2, we get
$\begin{align}
  & \Rightarrow \dfrac{{{130}^{\circ }}}{2}=\dfrac{2\angle QSR}{2} \\
 & \Rightarrow \angle QSR={{65}^{\circ }} \\
\end{align}$

Hence, the correct option is option A.

Note:
Here we have obtained the angle inside the quadrilateral. We need to know some important properties of quadrilaterals. The sum of all interior angles of a quadrilateral is four times the right angle. The diagonals of a quadrilateral intersect each other. The sum of all exterior angles of a quadrilateral is also four times the right angle.