Question

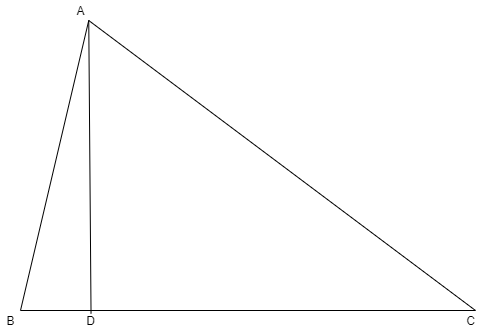
In the given figure below, \[AD\bot BC\] and \[BD=\dfrac{1}{3}CD\]Prove that
\[2A{{C}^{2}}=2A{{B}^{2}}+B{{C}^{2}}\].

Answer 1

Hint: Since there are right-angle triangles we mainly use all possible equations of right angle triangle that is ‘Pythagoras theorem’ (Pythagoras theorem is defined as the square of the hypotenuse is equal to the sum of squares of other two sides). That is for a triangle shown below the Pythagoras theorem can be applied as follows

Complete step by step answer:
Applying Pythagoras theorem for above figure, \[{{a}^{2}}={{b}^{2}}+{{c}^{2}}\]
Now try to make possible evaluations to convert all the obtained equations into the required equation that we want to prove.

Given that, \[BD=\dfrac{1}{3}CD\]
We know that,
\[BC=BD+DC\]
Now let us try to convert ‘BD’ and ‘DC’ in terms of ‘BC’ from the given data because we require the final equation in terms of’ BC’
Now, let us try to convert ‘DC’ in terms of ‘BC’ as follows
\[\begin{align}
  & \Rightarrow BC=BD+DC \\
 & \Rightarrow BC=\dfrac{1}{3}DC+DC\text{ (since BD=}\dfrac{1}{3}DC) \\
 & \Rightarrow BC=\dfrac{4}{3}DC \\
 & \Rightarrow DC=\dfrac{3}{4}BC \\
\end{align}\]
Similarly, let us try to convert ‘BD’ in terms of ‘BC’ as follows
\[\begin{align}
  & \Rightarrow BC=BD+DC \\
 & \Rightarrow BC=BD+3BD\text{ (Since BD = }\dfrac{1}{3}DC\text{ }\Rightarrow \text{ DC = 3BD)} \\
 & \Rightarrow BC=4BD \\
 & \Rightarrow BD=\dfrac{1}{4}BC \\
\end{align}\]

In a right-angled triangle, the Pythagoras theorem can be stated as ‘square of the hypotenuse (side opposite to right angle) is equal to the sum of squares of other two sides’.
That is for a triangle shown below the Pythagoras theorem can be applied as follows

Applying Pythagoras theorem for above figure, \[{{a}^{2}}={{b}^{2}}+{{c}^{2}}\]
Taking the figure given in the question, let us consider\[\Delta ADC\], by applying Pythagoras theorem we get
\[A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}\] ………..equation (i)
Now, let us consider \[\Delta ABD\], by applying Pythagoras theorem we get
\[A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}\] …………..equation (ii)
Now, subtracting equation (ii) from equation (i) we get
\[A{{C}^{2}}-A{{B}^{2}}=D{{C}^{2}}-B{{D}^{2}}\]
Now substituting the values of ‘DC’ and ‘BD’ in terms of ‘BC’ we got above
\[\begin{align}
  & \Rightarrow A{{C}^{2}}-A{{B}^{2}}={{\left( \dfrac{3}{4}BC \right)}^{2}}-{{\left( \dfrac{1}{4}BC \right)}^{2}} \\
 & \Rightarrow A{{C}^{2}}-A{{B}^{2}}=\dfrac{9}{16}B{{C}^{2}}-\dfrac{1}{16}B{{C}^{2}} \\
 & \Rightarrow A{{C}^{2}}-A{{B}^{2}}=\dfrac{8}{16}B{{C}^{2}} \\
 & \Rightarrow A{{C}^{2}}-A{{B}^{2}}=\dfrac{1}{2}B{{C}^{2}} \\
 & \Rightarrow A{{C}^{2}}=A{{B}^{2}}+\dfrac{1}{2}B{{C}^{2}} \\
\end{align}\]
Multiplying with ‘2’ on both sides we get
 \[2A{{C}^{2}}=2A{{B}^{2}}+B{{C}^{2}}\]
Hence proved

Note:
You need to be very careful in making calculations from the equations we obtained through the Pythagoras theorem we get confused sometimes while subtracting two equations.
That is instead of writing the equation \[A{{C}^{2}}-A{{B}^{2}}=D{{C}^{2}}-B{{D}^{2}}\], one get confused and writes \[A{{C}^{2}}-A{{B}^{2}}=B{{D}^{2}}-D{{C}^{2}}\]. So, you need to take care here.
Here, in this question we may have only two equations while in some other questions we may have more. So we need to be careful while evaluating the obtained equations.