Question

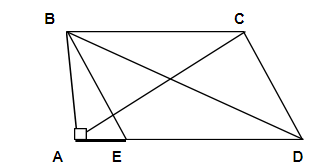
In the given figure, BEDC is a parallelogram.If the area of $\Delta ADC = 8$ and area of $\Delta BDC = 3$ and $\angle DAB = {90^ \circ }$ ,then the area of $\Delta AEB$ is

Answer 1

Hint: We know that the diagonal of a parallelogram split it into two triangles of same area.The area of parallelogram $\,\,area\,BCDE = 2 \times \, \Delta BDC = 2 \times 3 = 6$. Using this we can find the area of the triangle.

Complete step by step solution:
Step1:Also the area of the parallelogram is $DE \times AB.$
Step2: Therefore DE.AB=6
$\eqalign{
  & (AD-AE) \times AB = 6 \cr
  & AD.AB-AE.AB =6 \cr
& \Rightarrow \,\,\dfrac{1}{2}AD.AB \,-\, \dfrac{1}{2}AE.AB = 3 \,\,\,\,(dividing\,\,both\,\,sides\,\,by\,\,2) \cr
  & \Rightarrow \,\, \Delta ADC\,-\,\Delta AEB = 3 \,\,\,\,as\,\,height\,\,of\,\,\Delta ADC\,\,is\,\,nothing\,\,but\,\,AB \cr
  & \Rightarrow \,\, \Delta AEB\,=\,\Delta ADC - 3 \,\cr
 & \Rightarrow \Delta AEB\, =8-3\,\cr
 &\Rightarrow \,\Delta AEB\, =5 \cr } $
Therefore, the area of $\Delta AEB$ is 5 (in magnitude).

Note: A Parallelogram is a flat shape with opposite sides parallel and equal in length. Remember the area of parallelogram to solve these types of questions.