
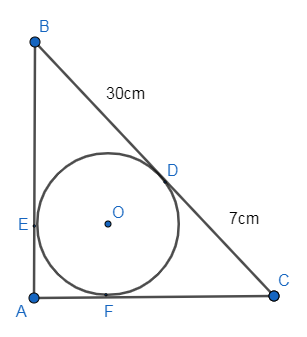
In the given figure, BDC is a tangent to the given circle at point D such that BD=30cm and CD=7cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle.
Calculate (i) AF (ii) radius of the circle.

Answer
551.1k+ views
Hint: In the given problem, we have to find the length of AF and the radius of the circle. Thus, we will use the circle-triangle property and the pythagoras theorem to get the solution. We will first let the value of AE and AF as x, then, we will find the value of x using the pythagorean theorem. For the radius of the circle, we will join the points OE and OF. Then, we get a square OEAF, and use the property of square, to get the required result for the solution.
Complete step by step solution:
According to the question, we have to find the length of AF and the radius of the circle.
Thus, we will use the circle-triangle property and the pythagoras theorem, to get the solution.
Given: BDC is the tangent of the circle, such that $BD=30cm$ and $DC=7cm$, ABC is a right angle triangle, right-angled at point A.
To find: (i) AF (ii) the radius of the circle.
So, first, we will find the value of AF.
As we know, the tangent-circle theorem is that if two tangent segments are drawn from the same external point, then the segments are equal. That is, BE and BD are the tangent segments drawn from the external point B, AE and AF are the tangents drawn from the external point A, and CF and CD. Thus, we get
Let $AE=AF=x$ ,
$BE=BD=30cm$ , and
$CF=CD=7cm$ ,
Then, we will get
$BE+EA=AB$
$\Rightarrow 30+x=AB$ ------- (1)
$BD+DC=BC$
$\Rightarrow 30+7=BC$
$\Rightarrow 37=BC$ --------- (2)
$AF+FC=AC$
$\Rightarrow x+7=AC$ -------- (3)
Therefore, from (1), (2), and (3), we get the value of sides AB, BC, and AB respectively. Now, we will apply the pythagoras theorem ${{(hypotenuse)}^{2}}={{(side)}^{2}}+{{(base)}^{2}}$ in triangle ABC, we get
$\Rightarrow {{(BC)}^{2}}={{(AB)}^{2}}+{{(AC)}^{2}}$
Thus, we will substitute the value of equation (1), (2), and (3) in the above equation, we get
$\Rightarrow {{(37)}^{2}}={{(30+x)}^{2}}+{{(x+7)}^{2}}$
On using the algebraic identity ${{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ in the above equation, we get
$\Rightarrow {{(37)}^{2}}=\left( 900+60x+{{x}^{2}} \right)+\left( {{x}^{2}}+14x+49 \right)$
Thus, on further simplification, we get
$\Rightarrow 1369=949+74x+2{{x}^{2}}$
We will subtract 1369 on both sides in the above equation, we get
$\Rightarrow 1369-1369=949+74x+2{{x}^{2}}-1369$
As we know, the same terms with opposite signs cancel out each other, therefore we get
$\Rightarrow 2{{x}^{2}}+74x-420=0$
Now, we will take common 2 on the left-hand side of the above equation, we get
$\Rightarrow 2\left( {{x}^{2}}+37x-210 \right)=0$
Now, we will divide 2 on both sides in the above equation, we get
$\Rightarrow \dfrac{2}{2}\left( {{x}^{2}}+37x-210 \right)=\dfrac{0}{2}$
On further simplification, we get
$\Rightarrow \left( {{x}^{2}}+37x-210 \right)=0$
Now, we will use splitting the middle term method. We will split the middle term as the addition of 42 and -5, because the product of these two numbers is equal to the product of ac.
Thus, we will write $37x=42x-5x$ , we get
$\Rightarrow {{x}^{2}}+42x-5x-210=0$
Now, we will take x common from the first two terms and -5 from the last two terms, we get
$\Rightarrow x\left( x+42 \right)-5\left( x+42 \right)=0$
So, we will take common (x+42) from the above equation, we get
$\Rightarrow \left( x+42 \right)\left( x-5 \right)=0$
Therefore, we get
$\Rightarrow \left( x+42 \right)=0$ and ----- (4)
$\Rightarrow \left( x-5 \right)=0$ -------- (5)
Now, we will solve equation (4), by subtracting 42 on both sides of the equation, we get
$\Rightarrow x+42-42=0-42$
As we know, the same terms with opposite signs cancel out each other, thus we get
$\Rightarrow x=-42$
Now, we will solve equation (5), by adding 5 on both sides of the equation, we get
$\Rightarrow x-5+5=0+5$
As we know, the same terms with opposite signs cancel out each other, thus we get
$\Rightarrow x=5$
Thus, we know that the side of the triangle is never negative, thus the negative value that is -42 is rejected.
Therefore, $AE=AF=x=5cm$
Now, we will solve (ii) the radius of the circle.
So, we will draw the figure by joining the lines OE and OF, we get
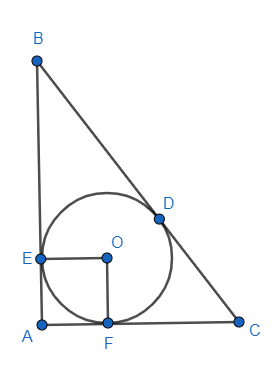
Now, we see that OEAF is a square, thus the sides of the square are equal to each other, that is
$OE=OF=FA=AE$
Also, we have found the value of AE and AF in (i) part, that is they are equal to 5cm. thus, we get
$OE=OF=FA=AE=5cm$
As OE is the radius of the circle. Therefore, the value of the radius of the circle is equal to 5cm.
Therefore, for the given problem, the value of AF is equal to 5cm and the value of the radius of the circle is equal to 5cm.
Note: While solving this problem, do mention the formulas you are using to avoid confusion and mathematical errors. Also, draw the figure to get an accurate answer. Here we also use the property of tangents such from an external point to the circle.
Complete step by step solution:
According to the question, we have to find the length of AF and the radius of the circle.
Thus, we will use the circle-triangle property and the pythagoras theorem, to get the solution.
Given: BDC is the tangent of the circle, such that $BD=30cm$ and $DC=7cm$, ABC is a right angle triangle, right-angled at point A.
To find: (i) AF (ii) the radius of the circle.
So, first, we will find the value of AF.
As we know, the tangent-circle theorem is that if two tangent segments are drawn from the same external point, then the segments are equal. That is, BE and BD are the tangent segments drawn from the external point B, AE and AF are the tangents drawn from the external point A, and CF and CD. Thus, we get
Let $AE=AF=x$ ,
$BE=BD=30cm$ , and
$CF=CD=7cm$ ,
Then, we will get
$BE+EA=AB$
$\Rightarrow 30+x=AB$ ------- (1)
$BD+DC=BC$
$\Rightarrow 30+7=BC$
$\Rightarrow 37=BC$ --------- (2)
$AF+FC=AC$
$\Rightarrow x+7=AC$ -------- (3)
Therefore, from (1), (2), and (3), we get the value of sides AB, BC, and AB respectively. Now, we will apply the pythagoras theorem ${{(hypotenuse)}^{2}}={{(side)}^{2}}+{{(base)}^{2}}$ in triangle ABC, we get
$\Rightarrow {{(BC)}^{2}}={{(AB)}^{2}}+{{(AC)}^{2}}$
Thus, we will substitute the value of equation (1), (2), and (3) in the above equation, we get
$\Rightarrow {{(37)}^{2}}={{(30+x)}^{2}}+{{(x+7)}^{2}}$
On using the algebraic identity ${{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ in the above equation, we get
$\Rightarrow {{(37)}^{2}}=\left( 900+60x+{{x}^{2}} \right)+\left( {{x}^{2}}+14x+49 \right)$
Thus, on further simplification, we get
$\Rightarrow 1369=949+74x+2{{x}^{2}}$
We will subtract 1369 on both sides in the above equation, we get
$\Rightarrow 1369-1369=949+74x+2{{x}^{2}}-1369$
As we know, the same terms with opposite signs cancel out each other, therefore we get
$\Rightarrow 2{{x}^{2}}+74x-420=0$
Now, we will take common 2 on the left-hand side of the above equation, we get
$\Rightarrow 2\left( {{x}^{2}}+37x-210 \right)=0$
Now, we will divide 2 on both sides in the above equation, we get
$\Rightarrow \dfrac{2}{2}\left( {{x}^{2}}+37x-210 \right)=\dfrac{0}{2}$
On further simplification, we get
$\Rightarrow \left( {{x}^{2}}+37x-210 \right)=0$
Now, we will use splitting the middle term method. We will split the middle term as the addition of 42 and -5, because the product of these two numbers is equal to the product of ac.
Thus, we will write $37x=42x-5x$ , we get
$\Rightarrow {{x}^{2}}+42x-5x-210=0$
Now, we will take x common from the first two terms and -5 from the last two terms, we get
$\Rightarrow x\left( x+42 \right)-5\left( x+42 \right)=0$
So, we will take common (x+42) from the above equation, we get
$\Rightarrow \left( x+42 \right)\left( x-5 \right)=0$
Therefore, we get
$\Rightarrow \left( x+42 \right)=0$ and ----- (4)
$\Rightarrow \left( x-5 \right)=0$ -------- (5)
Now, we will solve equation (4), by subtracting 42 on both sides of the equation, we get
$\Rightarrow x+42-42=0-42$
As we know, the same terms with opposite signs cancel out each other, thus we get
$\Rightarrow x=-42$
Now, we will solve equation (5), by adding 5 on both sides of the equation, we get
$\Rightarrow x-5+5=0+5$
As we know, the same terms with opposite signs cancel out each other, thus we get
$\Rightarrow x=5$
Thus, we know that the side of the triangle is never negative, thus the negative value that is -42 is rejected.
Therefore, $AE=AF=x=5cm$
Now, we will solve (ii) the radius of the circle.
So, we will draw the figure by joining the lines OE and OF, we get

Now, we see that OEAF is a square, thus the sides of the square are equal to each other, that is
$OE=OF=FA=AE$
Also, we have found the value of AE and AF in (i) part, that is they are equal to 5cm. thus, we get
$OE=OF=FA=AE=5cm$
As OE is the radius of the circle. Therefore, the value of the radius of the circle is equal to 5cm.
Therefore, for the given problem, the value of AF is equal to 5cm and the value of the radius of the circle is equal to 5cm.
Note: While solving this problem, do mention the formulas you are using to avoid confusion and mathematical errors. Also, draw the figure to get an accurate answer. Here we also use the property of tangents such from an external point to the circle.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




