Question

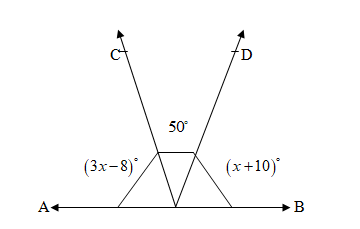
In the given figure AOB is a straight line,$\angle AOC = {\left( {3x - 8} \right)^ \circ }$,$\angle COD = {50^ \circ }$and$\angle BOD = {\left( {x + 10} \right)^ \circ }$ . The value of $x$ is
a)32
b)42
c)36
d)52

Answer 1

Hint: Here, we will use the property of the straight line. We will add all the angles and equate it to the sum of angles in a straight line. Then we will simplify it further to find the value of $x$. A straight line is a line with two endpoints and is exactly half of a revolution.

Complete step-by-step answer:
We have the value of all the angles in a straight line bisected by two rays.
It is given that
$\angle AOC = {\left( {3x - 8} \right)^ \circ }$……$\left( 1 \right)$
$\angle COD = {50^ \circ }$…….$\left( 2 \right)$
$\angle BOD = {\left( {x + 10} \right)^ \circ }$……..$\left( 3 \right)$
We know that the sum of all the angles in the same side of a straight line is ${180^ \circ }$.
Therefore, on adding all the three equation given above, we will get
$\angle AOC + \angle COD + \angle BOD = {\left( {3x - 8} \right)^ \circ } + {50^ \circ } + {\left( {x + 10} \right)^ \circ }$
Substituting ${180^ \circ }$ on left side, we get
$ \Rightarrow {180^ \circ } = 3x - {8^ \circ } + {50^ \circ } + x + {10^ \circ }$
Adding and subtracting the like terms, we get
$ \Rightarrow {180^ \circ } = 4x + {52^ \circ }$
Subtracting \[{52^ \circ }\] from both the sides, we get
$ \Rightarrow 4x = {180^ \circ } - {52^ \circ }$
Dividing both side by 4, we get
$ \Rightarrow x = \dfrac{{{{128}^ \circ }}}{4}$
$ \Rightarrow x = {32^ \circ }$
Hence, option (a) is correct.

Note: When two rays join on a straight line they make an angle and the point where they meet in the straight line is known as the vertex. A straight line can be formed by joining two right angles as their sum will be equal to ${180^ \circ }$. Straight-line having no rays or a straight angle is also known as ‘flat angle’.