Question

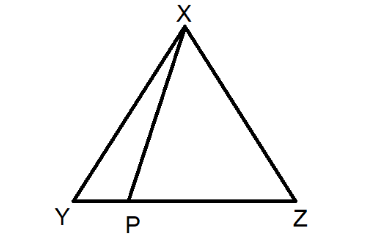
In the given figure $ \angle YXZ=\angle XPZ $ , then $ \dfrac{ZX}{ZY} $ is equal to

A. $ ZY\times ZP $
B. $ X{{Z}^{2}} $
C. $ \dfrac{PZ}{XZ} $
D. $ P{{Z}^{2}} $

Answer 1

Hint: We first find the same angles between the $ \Delta XYZ $ and $ \Delta XPZ $ . Based on the same angles we find the ratio of the similar sides. We form the relation and find the solution for $ \dfrac{ZX}{ZY} $ .

Complete step by step solution:
We are going to use the concept of similar triangles and then use the ratio of the sides of those triangles.
In the given figure we have two triangles where we take $ \Delta XYZ $ and $ \Delta XPZ $ .
It’s given that $ \angle YXZ=\angle XPZ $ . Also $ \angle XZY=\angle XZP $ is the common angle.
We also know that the sum of three angles of a triangle is always equal to $ {{180}^{\circ }} $ .
We got two angles of each triangle being equal which means the remaining angle of each triangle is also equal.
So, $ \angle XYZ=\angle PXZ $ .
We know that if three angles of two triangles are the same then the triangles are similar triangles and the ratio of opposite sides of similar angles are equal.
Therefore, for $ \Delta XYZ $ and $ \Delta XPZ $ we get $ \dfrac{ZX}{PZ}=\dfrac{ZY}{XZ}=\dfrac{XY}{XP} $ .
We take $ \dfrac{ZX}{PZ}=\dfrac{ZY}{XZ} $ and get $ \dfrac{ZX}{ZY}=\dfrac{PZ}{XZ} $ .
The correct option is C.
So, the correct answer is “Option C”.

Note: The concept of similar triangles and congruent triangles are two different terms that are closely related. Similar triangles are two or more triangles with the same shape, equal pair of corresponding angles and the same ratio of the corresponding sides. In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection.