Question

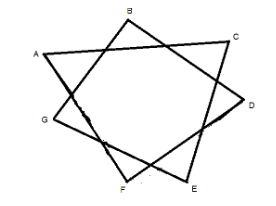
In the given figure \[\angle \left( {A + B + C + D + E + F + G} \right) = \]

A) \[{360^ \circ }\]
B) \[{500^ \circ }\]
C) \[{520^ \circ }\]
D) \[{540^ \circ }\]

Answer 1

Hint: Here first we will calculate the sum of all angles of a regular heptagon and then will find the measure of each angle of heptagon and then we will apply the linear angle property of triangles which states that the sum of two adjacent angles formed by two intersecting lines is \[{180^ \circ }\] and then find the sum of all angles and get the desired answer.

Complete step-by-step answer:
Here HIJKLMN is a heptagon and has 7 sides.
Now we know that, the sum of all angles of a polygon with n sides is given by:-
\[\left( {n - 2} \right) \times {180^ \circ }\]
Therefore, putting the value of n as 7 we get:-
\[sum = \left( {7 - 2} \right) \times {180^ \circ }\]
Solving it further we get:-
\[sum = \left( 5 \right) \times {180^ \circ }\]
\[ \Rightarrow sum = {900^ \circ }\]
Therefore, the sum of all angles of a regular pentagon is \[{900^ \circ }\]
Hence, the measure of each angle of heptagon is:-
\[{\text{one angle}} = \dfrac{{{{900}^ \circ }}}{7}\]
Solving it we get:-
\[{\text{one angle}} = {128.57^ \circ }\]
This implies, \[\angle NHI = \angle HIJ = \angle IJK = \angle JKL = \angle KLM = \angle LMN = \angle MNH = {128.57^ \circ }\]
Now we know that, \[\angle NHI\]and \[\angle AHN\]are forming a linear pair.
Therefore, applying the linear pair property we get:
\[\angle NHI + \angle AHN = {180^ \circ }\]
Putting in the respective value we get:-
\[{128.57^ \circ } + \angle AHN = {180^ \circ }\]
Solving it further we get:-
\[\angle AHN = {180^ \circ } - {128.57^ \circ }\]
\[\angle AHN = {51.43^ \circ }\]
Similarly, \[\angle MNH\]and \[\angle ANH\] are forming a linear pair.
Therefore, applying the linear pair property we get:
\[\angle MNH + \angle ANH = {180^ \circ }\]
Putting the respective value we get:-
\[128.5 + \angle ANH = {180^ \circ }\]
Solving it further we get:-
\[\angle ANH = {180^ \circ } - {128.57^ \circ }\]
\[ \Rightarrow \angle ANH = {51.43^ \circ }\]
Now in triangle AHN,
\[\angle ANH = {51.43^ \circ }\]
\[\angle AHN = {51.43^ \circ }\]
Applying angle sum property of triangle which states that the sum of all angles of a triangles is \[{180^ \circ }\]
Therefore, in \[\Delta AHN\] we get:-
\[\angle ANH + \angle AHN + \angle NAH = {180^ \circ }\]
Putting respective values we get:-
\[{51.43^ \circ } + {51.43^ \circ } + \angle NAH = {180^ \circ }\]
Solving it further we get:-
\[{102.86^ \circ } + \angle NAH = {180^ \circ }\]
\[\angle NAH = {180^ \circ } - {102.86^ \circ }\]
Solving it further we get:-
\[\angle NAH = {77.14^ \circ }\]
Similarly, \[\angle HBI = \angle ICJ = \angle JDK = \angle KEL = \angle LFM = \angle MGN = {77.14^ \circ }\]
Hence, \[\angle A = \angle B = \angle C = \angle D = \angle E = \angle F = \angle G = {77.14^ \circ }\]
Now adding each angle we get:-
\[\angle A + \angle B + \angle C + \angle D + \angle E + \angle F + \angle G = 7 \times {77.14^ \circ }\]
Solving this further we get:-
\[\angle A + \angle B + \angle C + \angle D + \angle E + \angle F + \angle G = {539.98^ \circ } \sim {540^ \circ }\]

Therefore, option D is the correct option.

Note: Students can also use the following formula to find the sum of all angles of a regular polygon of side n:-
\[\left( {n - 2} \right) \times {180^ \circ }\]
Also, the students should note that all the angles and sides of a regular polygon are equal.