Question

In the given figure $ \angle DAB={{90}^{\circ }} $ , then find the area of the field.

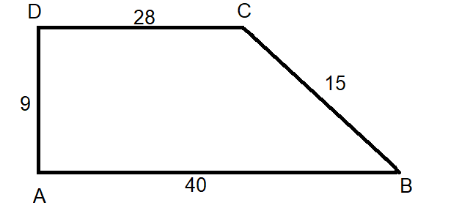
A. $ 208\text{ }{{\text{m}}^{2}} $
B. $ 402\text{ }{{\text{m}}^{2}} $
C. $ 300\text{ }{{\text{m}}^{2}} $
D. $ 306\text{ }{{\text{m}}^{2}} $
E. none of these

Answer 1

Hint: We first divide the whole area into different parts, one being a rectangle and the other one being a right-angle triangle. We find their individual areas. Then we add them to find the total area of the full part.

Complete step by step solution:
We first draw a perpendicular from point C on the line AB which intersects AB at point E.

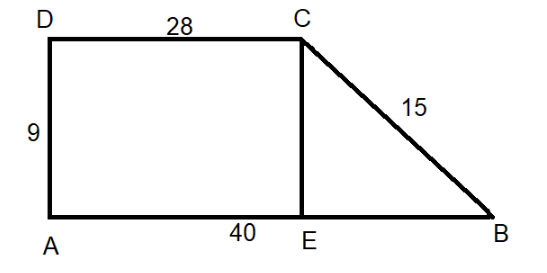
As $ \angle DAB=\angle CEA={{90}^{\circ }} $ , the quadrilateral AECD becomes the rectangle. Therefore, the opposite sides are equal. We get $ DC=AE;AD=EC=9 $ .
 The $ \Delta BCE $ is a right-angle triangle whose $ \angle CEB={{90}^{\circ }} $ .
We now find the area of the two figures separately.
The rectangle has two consecutive sides with lengths of 28 and 9.
The area of the rectangle is $ 28\times 9=252 $ square meter.
The length of EB will be $ EB=AB-AE=40-28=12 $ meter.
Now for the right-angle triangle the area will be $ \dfrac{1}{2}\times 12\times 9=54 $ square meter.
The total area will be $ 252+54=306 $ square meter.
The correct option is D.
So, the correct answer is “Option D”.

Note: We used the theorem of $ \dfrac{1}{2}\times base\times height $ for the area of the right-angle triangle. For the rectangle we used the concept of $ length\times breadth $ . We also could have used the diagonal concept to find the full area.