Question

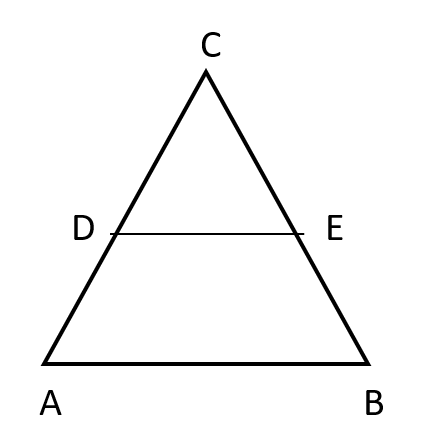
In the given figure, $\angle A = \angle B$and $AD = BE.$Show that $DE\parallel AB.$

Answer 1

Hint: In this question we will use given data to show that $DE$ is parallel to $AB$. Since $\angle A$ is equal to $\angle B$ hence the given triangle $ABC$ is an isosceles triangle. In this question the converse of Basic proportionality theorem is used. It says that if a line$\left( {DE} \right)$ divides any two sides ($AC$and$BC$) of a triangle in the same ratio, then the line must be parallel to the third side$\left( {DE\parallel AB} \right)$.

Complete step by step solution:
In a given figure,
$\angle A = \angle B$
$AD = BE.$
$ \Rightarrow $$\vartriangle ABC$is an Isosceles triangle.
Then, $AC = BC$ (triangle is isosceles)
$
  AD + DC = BE + EC \\
  AD + DC = AD + EC \\
 $
                                            ------ ($AD = BE$ is given)
$\therefore DC = EC$
$ \Rightarrow \dfrac{{DC}}{{EC}} = 1$ --- $1$
Also $AD = BE$
$\dfrac{{AD}}{{BE}} = 1$ --- $2$
From $1$ and$2$, we have
$\dfrac{{DC}}{{EC}} = \dfrac{{AD}}{{BE}}$
Hence, by converse of basic proportionality theorem
$ \Rightarrow DE\parallel AB$
Hence proved.

Note: In the given diagram we proved that $AC$ and $BC$ are of equal length hence angle $A$ and angle $D$ are corresponding angles, similarly angle $B$ is corresponding with angle $E$. Generally the students will make a mistake while finding the type of triangle, so we had given angle A is equal to angle B, So the sides opposite to equal angles of a triangle are equal and the triangle is isosceles.