Question

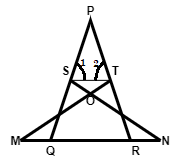
In the given figure \[\angle 1 = \angle 2\] and \[\Delta NSQ \cong \Delta MTR\], then prove that \[\Delta PTS \sim \Delta PRQ\].

Answer 1

Hint: In the given question, we have to prove the similarity of two triangles (which means that the triangles are similar in shape, but not necessarily equal). For doing that we have to show that either of the three necessary conditions are true – two corresponding angles are equal (AA), two corresponding sides and the included angle is equal (SAS), or all the three sides are equal (SSS). Here, we have been given that two other triangles are congruent (which means that the two triangles are similar in shape and equal in too), so we can use that to show the similarity by showing the sides of the congruent triangles equal and using that to prove the equality of the triangles.

Complete step-by-step answer:
In the given question, we have been given:
\[\angle 1 = \angle 2\] and \[\Delta NSQ \cong \Delta MTR\]
We have to prove:
\[\Delta PTS \sim \Delta PRQ\]

Now, \[\Delta NSQ \cong \Delta MTR\]
So, \[\angle NQS = \angle MRT\] (cpct)
or, if we see the two angles from the point of view of the big triangle \[\Delta PQR\], we get:
\[ \Rightarrow \]\[\angle PQR = \angle PRQ\] …(i)
Now, in \[\Delta PST\], we have:

\[\angle 1 + \angle 2 + \angle SPT = 180^\circ \]
Now, \[\angle 1 = \angle 2\]
So, \[\angle 1 + \angle 1 + \angle SPT = 180^\circ \]
or, \[2\angle 1 + \angle SPT = 180^\circ \] …(ii)

Now in \[\Delta PQR\], we have:
\[\angle PQR + \angle PRQ + \angle QPR = 180^\circ \]
Now, \[\angle PQR = \angle PRQ\] (from (i))
So, \[\angle PQR + \angle PQR + \angle QPR = 180^\circ \]
or, \[2\angle PQR + \angle QPR = 180^\circ \]
Now, \[\angle QPR = \angle SPT\] (same angle)
So, \[2\angle PQR + \angle SPT = 180^\circ \] …(iii)

Now, comparing equations (ii) and (iii), we have:
\[ \Rightarrow \] \[\angle 1 = \angle PQR\] …(iv)

Now, in \[\Delta PTS\] and \[\Delta PRQ\], we have:
\[ \Rightarrow \] \[\angle P = \angle P\] (common angle)
\[ \Rightarrow \] \[\angle PST = \angle PQR\] (from (iv))
Hence, \[\Delta PTS \sim \Delta PRQ\] (AA similarity)
Hence, proved.

Note: So, we saw that in solving questions like these, we must first see what all has been given to us and write it down. Then, we need to write down what has been given to us. Then, we see if with what has been given to us, we can use some information or deduce some comprehensible information to prove what we need to prove. Like in this question, we used the information that sides of any two congruent triangles is equal and we then used this information to prove the similarity of the required two triangles. It is a point to note that if two triangles are congruent, then it is always true that they are similar too. But, if two triangles are only similar, then it is not always true that they are congruent too.