Question

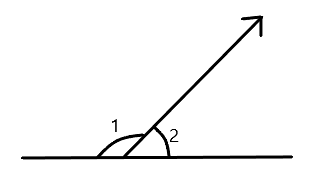
In the given figure $\angle 1$ and $\angle 2$ are supplementary angles. If $\angle 1$ is decreased, what changes should take place in $\angle 2$ so that both the angles still remain supplementary?

Answer 1

Hint: In the above question we have been given two supplementary angles. We know that if two angles are supplementary then the sum of both angles is
$180^\circ $ . So we will use this property to solve this question. We will assume that let $\angle 1$ be decreased by $x$ .

Complete step-by-step solution:
We have been given that figure $\angle 1$ and $\angle 2$ are supplementary angles.
So it can be written as
$\angle 1 + \angle 2 = 180^\circ $
We can calculate $\angle 1$ as,
 $\angle 1 = 180^\circ - \angle 2$
Now let us assume that $\angle 1$ is decreased by $x$ .
It can be written as
 $\left( {\angle 1 - x} \right)$
Now since both the angles are supplementary, so if there is a change in $\angle 1$ , then the other angle will also change.
So let us say that $\angle 2$ changes to $\angle 3$ .
So we have new angles i.e.
$\left( {\angle 1 - x} \right)$ and $\angle 3$ area also supplementary angles.
So we can write them as
 $\left( {\angle 1 - x} \right) + \angle 3 = 180^\circ $
We can substitute the value $\angle 1 = 180^\circ - \angle 2$ in the equation, so we have
$180^\circ - \angle 2 - x + \angle 3 = 180^\circ $
By arranging the terms in the right hand side, we have
$\angle 3 = 180^\circ - 180^\circ + \angle 2 + x$
It gives us value
$\angle 3 = \angle 2 + x$
So we can see that the other angle i.e. $\angle 2$ is increased by $x$
Hence in order to make both the angles supplementary if $\angle 1$ is decreased by any value , then $\angle 2$ is to be increased by the same value.

Note: We should know the properties of supplementary angles to solve this type of question. We should note that if one angle is $90^\circ $ , then the other angle has to be equal to $90^\circ $ . Another property is that if one angle is acute angle then the other angle has to be an obtuse angle to fulfil the criteria of supplementary angle.