Question

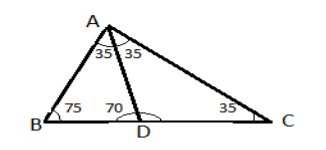
In the given figure AD bisects $\angle A$. Arrange AB, BC and DC in ascending order.

A) $BC>DC>AB$
B) $AB>DC>BC$
C) $BC>AB>DC$
D) $DC>AB>BC$

Answer 1

Hint: Exterior angle theorem : Exterior angle is greater than interior opposite angle.
In a triangle, the side opposite to the greater angle is longer.
Sides opposite to equal angles are equal.
To find the comparison between the sides of the triangle, we can make use of the angles provided and find a relationship between these angles and needed sides.

Complete step-by-step answer:
Step 1: (b) and (d) are wrong.
A result which we can deduce only by looking into the figure is the comparison between the sides DC and BC.
As D is a point on the side BC, DC will be always less than BC : DCStep 2: (a) is correct
Now we will compare the given angles and find the relation between needed sides.
As angle opposite to equal angles are equal, in $\vartriangle ADC$ $\angle DAC = \angle C = {35^0}$ . Thus their opposite sides AD and DC are equal.
In $\vartriangle ABD$, AD is the greatest among AB and BD, as AD is opposite to the largest angle $\angle B = {75^0}$.
Implies DC is greater than AB and BD. Thus we get DC>AB --------formula2
From formula1 and formula2, we get the relation BC>DC>AB
Step3: (c) is wrong
As DC is the side opposite to largest angle in the triangle, DC>AB

Option (a) BC>DC>AB is correct

Note: Exterior angle theorem actually states that the exterior angle of a triangle is equal to sum of opposite interior angles.In a scalene triangle, all the side length may be different. But can be compared with the angles enclosed. Side opposite to the largest angle is greater and the side opposite to the smallest angle is smaller.
Errors can occur in the above comparison among sides of two triangles within a triangle.
Exterior angle theorem can be used in between for comparison among angles.