Question

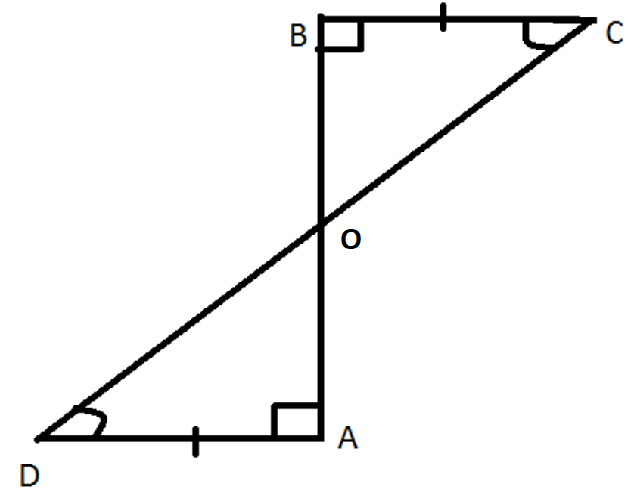
In the given figure $AD$ and $BC$ are equal perpendiculars to a line segment $AB$. Show that $CD$ bisects $AB$.

Answer 1

Hint: 1. If two lines are perpendicular to a single line on its two ends then the perpendicular lines are equal. Just like in the figure given to us line $BC$ and $AD$ are perpendicular on line $AB$, and since the distance between $BC$ and $AD$ will never change they are said to be parallel lines.
2. When a line intersects two parallel lines then the alternate interior angles are equal.
I.e. if taken an example of above figure,
$CD$ Intersects lines $BC$ and $AD$.
Therefore, $\angle BCO = \angle ADO$ because they are alternate interior angles.

Complete step by step answer:
 1. We are provided by the information,
$AD$ = $BC$
And, $AD$ and $BC$ are perpendicular to line $AB$.
2. And, we have to prove:
$CD$ Bisects $AB$
i.e. $AO = BO$
3. Looking into the $\Delta AOD$ and $\Delta BOD$:
$\angle DAO = \angle CBO$ (Each of the angle is $90^{\circ}$)
$AD$ = $BC$ (As given in the question)
$\angle BCO = \angle ADO$ (Alternate interior angles are equal)
Therefore, By using the ASA (Angle Side Angle) property of congruence,
$\Delta AOD \cong \Delta BOD$
4. And since, parts of two congruent triangles can be said to be equal.
$AO = BO$
Which states that $CD$ bisects $AB$.

Note: Another approach could have been taken by using the vertically opposite angle property of triangles.
At point O, $\angle AOD = \angle BOC$ because they are formed by the intersection of two two lines.