Question

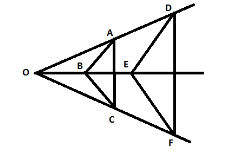
In the given figure $ AB\parallel DE $ and $ BC\parallel EF $ . Prove that $ AC\parallel DF $

Answer 1

Hint: In this question, it has been given that $ AB\parallel DE $ and $ BC\parallel EF $ . We need to prove that $ AC\parallel DF $ . We will prove this condition, by using basic proportionality theorem and converse of basic proportionality theorem. We are using BPT because here the triangles are similar.

Complete step-by-step answer:
It has been given that $ AB\parallel DE $
We know that, if a line is drawn parallel to one side of a triangle intersecting the other two sides on distinct points, then the other two sides are divided in the same ratio. This is called the basic proportionality theorem (BPT).
Therefore, by basic proportionality theorem, we have,
  $ \dfrac{{OA}}{{OD}} = \dfrac{{OB}}{{OE}} $
Let it be equation 1
It is also given that $ BC\parallel EF $
Therefore, by basic proportionality theorem, we have,
  $ \dfrac{{OC}}{{OF}} = \dfrac{{OB}}{{OE}} $
Let it be equation 2
Comparing the equations 1 and 2, we have,
 $ \dfrac{{OC}}{{OF}} = \dfrac{{OA}}{{OD}} $
Now, we know that, if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. This is known as converse of basic proportionality theorem.
Therefore, by converse of basic proportionality theorem, we can say that,
 $ AC\parallel DF $
Hence, proved that $ AC\parallel DF $ .
So, the correct answer is “$ AC\parallel DF $”.

Note: In this question, it is important to note here that if the two triangles are similar then we can use the basic proportionality theorem. When the two triangles are similar then, corresponding angles of both the triangles are equal and corresponding sides of both the triangles are proportional to each other. Basic proportionality theorem is also known as Thales theorem because BPT was introduced by a famous Greek Mathematician, Thales. The converse of any theorem is just a reverse of the original theorem, just like we have active and passive voices in English.