
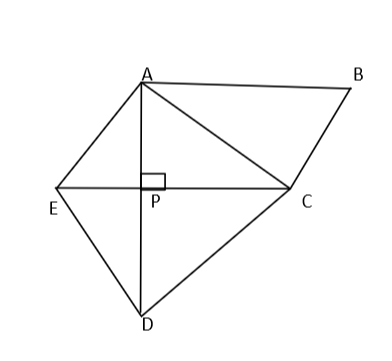
In the given figure, ABCE is a parallelogram. P is the midpoint of AD and AD \[ \bot \] EC. If AD=20cm and EC=18cm, find the area of the given figure.
A.$300cm_{}^2$
B.$280cm_{}^2$
C.$270cm_{}^2$
D.$290cm_{}^2$

Answer
598.5k+ views
Hint: To do this type of question one should know about the area of triangle and area of parallelogram. You should know the properties of a midpoint. If an angle is given like right angle then the area for a right angle triangle can be changed i.e. $\left( {\dfrac{1}{2} \times B \times H} \right)$ where B= Base, H=height. So to initialize these types of questions, firstly write all the dimensions you are given with and then write down the figure you are given with and then write the formulae of the area of those figures.
Complete step-by-step solution:
Given, ABCE is a parallelogram
P is a mid point so $AP = PD$
AD is perpendicular to EC.
$AD = 20cm$and $EC = 18cm$
To find = Area of the whole given figure
As P is the mid point so
$AP = PD = \dfrac{1}{2} \times AD$
$AP = PD = \dfrac{1}{2} \times 20 = 10cm$ $\therefore AD = 20cm$
Area of parallelogram = The perpendicular height in parallelogram $ \times $ The base to which height is perpendicular
$
= EC \times AP \\
= 18cm \times 10cm = 180cm_{}^2 \\
$
Area of triangle ECD $
= \dfrac{1}{2} \times Base \times Height \\
= \dfrac{1}{2} \times 18 \times 10 = 90cm_{}^2 \\
$
Area of the whole figure = Area of triangle + Area of parallelogram
$
= 180 + 90 \\
= 270cm_{}^2 \\
$
So the correct option is C i.e. $270cm_{}^2$
Note: In a right angle triangle the line which is directly seen opposite to ${90^ \circ }$ angle or right angle that is known as the hypotenuse of triangle and other two sides which are left is base and height according to the other two angles. One can make a mistake during the area of parallelogram. We have to take the perpendicular height from any one line of parallelogram then the base that we require in the area should be that to which we have taken the perpendicular height.
Complete step-by-step solution:

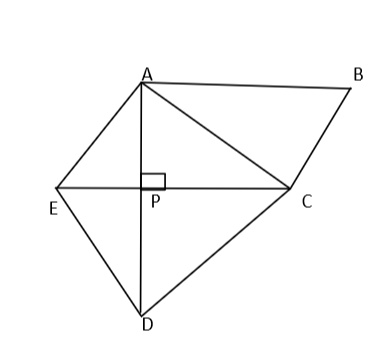
Given, ABCE is a parallelogram
P is a mid point so $AP = PD$
AD is perpendicular to EC.
$AD = 20cm$and $EC = 18cm$
To find = Area of the whole given figure
As P is the mid point so
$AP = PD = \dfrac{1}{2} \times AD$
$AP = PD = \dfrac{1}{2} \times 20 = 10cm$ $\therefore AD = 20cm$
Area of parallelogram = The perpendicular height in parallelogram $ \times $ The base to which height is perpendicular
$
= EC \times AP \\
= 18cm \times 10cm = 180cm_{}^2 \\
$
Area of triangle ECD $
= \dfrac{1}{2} \times Base \times Height \\
= \dfrac{1}{2} \times 18 \times 10 = 90cm_{}^2 \\
$
Area of the whole figure = Area of triangle + Area of parallelogram
$
= 180 + 90 \\
= 270cm_{}^2 \\
$
So the correct option is C i.e. $270cm_{}^2$
Note: In a right angle triangle the line which is directly seen opposite to ${90^ \circ }$ angle or right angle that is known as the hypotenuse of triangle and other two sides which are left is base and height according to the other two angles. One can make a mistake during the area of parallelogram. We have to take the perpendicular height from any one line of parallelogram then the base that we require in the area should be that to which we have taken the perpendicular height.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




