Question

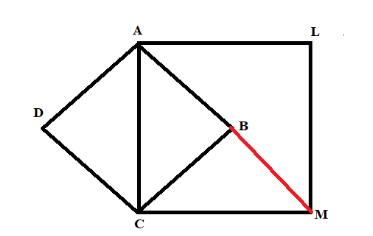
In the given figure ABCD is rhombus and ALMC is square, AC=BC. Find the ∠MBC.

A. ${60^0}$
B. ${75^0}$
C. ${30^0}$
D. ${45^0}$

Answer 1

HINT- Proceed the solution of this question first using the side properties of rhombus and square find the relation between the different sides and the angles i.e. angles of equilateral triangle (${60^0}$) and at last get the relation between all three angles of triangle so that we can apply the condition i.e. sum of all angle of a triangle = ${180^0}$ hence we can find the unknown angle.

Complete step-by-step answer:

In the question it is given that ABCD is rhombus and ALMC is square, AC=BC as we have shown in the figure below.

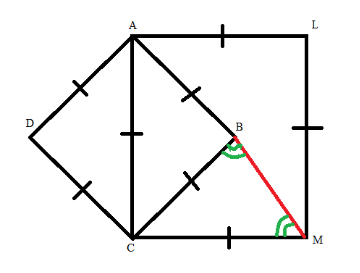
In the square ALMC, ∠ACM = ${90^0}$ because all the angle of square equal to ${90^0}$
Also, AC=BC (Given)
and BC=AB (Sides of Rhombus)
Therefore, AB=BC=AC
Hence if all the sides of a triangle are equal then it will be an equilateral triangle.

So, △ABC is an equilateral triangle
And we know that each angle of an equilateral triangle equal to ${60^0}$
Now, ∠ACB=${60^0}$

So from figure, we can write,
⇒∠ACM = ${90^0}$
⇒∠ACB +∠BCM = ${90^0}$


⇒${60^0}$ +∠BCM = ${90^0}$


⇒∠BCM OR ∠MCB=${90^0}$−${60^0}$=${30^0}$
Now in triangle MBC,
⇒BC=CM,

Hence by the property of a triangle, if two sides are equal then corresponding angles opposite to those sides of a triangle are also equal.

So ∠MBC=∠BMC=x(let)
Sum of all angle of a triangle = ${180^0}$
⇒∠MCB+∠MBC+∠BMC= ${180^0}$

So on putting these values of angles
⇒${30^0}$+x+x= ${180^0}$
⇒2x=${180^0} - {30^0}$
⇒x=$\dfrac{{{{150}^0}}}{2} = {75^0}$

Hence, ∠MBC $ = {75^0}$

Note- Whenever we came up of such types of question, we should mainly focus on the diagram and its construction because with the proper understanding of figure we can bring out more result and can find the correct step to start the question as in the above question rhombus is sharing its diagonal as one of the side of square, hence with this much of visualisation and given condition AC=BC, We can say all the sides of a given figure will be zero and it there will be formation of an equilateral triangle whose angles will be known. Hence such a type of good understanding of figures will lead us to the correct answer.