
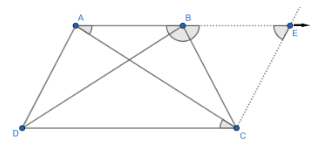
In the given figure $ABCD$ is a trapezium in which $AB\parallel CD$ and $AD=BC$ . Show that both diagonal are equal, $AC=BD$ .

Answer
607.8k+ views
Hint: For solving this problem first we will prove that $\angle DAB=\angle CBA$ . Then we will prove two triangles congruent using side angle side congruence rule. Then, we will finally show that the diagonals of the given trapezium are equal.
Complete step by step answer:
Given:
We have trapezium $ABCD$ in which $AB\parallel CD$ and $AD=BC$ .
Construction: Draw a line parallel to $AD$ through $C$ and extend the segment $AB$ to meet the line drawn through $C$ . Let they intersect at a point $E$ .
Now, as it is given that $AB\parallel CD$ so $AE\parallel CD$ and by construction, we can say that $AD\parallel CE$ . Then, $AECD$ is a quadrilateral in which opposite sides are parallel so, $AECD$ will be a parallelogram. Then, $AD=CE$ as opposite sides of the parallelogram are equal.
Now, consider $\Delta BCE$ we can write that, $AD=BC=CE$ . So, the $\Delta BCE$ is an isosceles triangle in which $BC=CE$ . As we know that in an isosceles triangle angles opposite to equal sides of an isosceles triangle are equal. Then,
$\angle CBE=\angle CEB.........\left( 1 \right)$
Now, as by construction $AE\parallel CD$ and $AE$ in the transversal then, interior angles on the same side of the transversal are supplementary angles. Then,
$\begin{align}
& \angle DAB+\angle CEB={{180}^{0}} \\
& \Rightarrow \angle DAB={{180}^{0}}-\angle CEB \\
\end{align}$
Now, using the equation in the above equation. Then,
$\begin{align}
& \angle DAB={{180}^{0}}-\angle CEB \\
& \Rightarrow \angle DAB={{180}^{0}}-\angle CBE...............\left( 2 \right) \\
\end{align}$
Now, as $AE$ is a straight line, so $\angle CBA$ and $\angle CBE$ will be linear pairs. Then,
$\begin{align}
& \angle CBA+\angle CBE={{180}^{0}} \\
& \Rightarrow \angle CBA={{180}^{0}}-\angle CBE............\left( 3 \right) \\
\end{align}$
Now, comparing equation (2) and equation (3). Then,
$\begin{align}
& \angle DAB={{180}^{0}}-\angle CBE=\angle CBA \\
& \Rightarrow \angle DAB=\angle CBA..............\left( 4 \right) \\
\end{align}$
Now, consider $\Delta ABD$ and $\Delta BAC$ . Then,
$\begin{align}
& AB=BA\text{ }\left( common \right) \\
& \angle DAB=\angle CBA\text{ }\left( from\text{ 4} \right) \\
& AD=BC\text{ }\left( Given \right) \\
\end{align}$
Now, by the side angle side congruence rule we can write that $\Delta ABD\cong \Delta BAC$ . And as we know that in a pair of congruent triangles corresponding sides of the triangle are equal. Then, $AD=BC$ .
Thus, we have proved that diagonals of the given trapezium are equal in length.
Hence, proved.
Note: Here, the student must take care of the geometrical properties of the parallelogram. Moreover, be careful in writing the name of congruent triangles. For example in this question we cannot write that $\Delta ADB\cong \Delta BAC$ , the correct way is $\Delta ABD\cong \Delta BAC$ .
Complete step by step answer:
Given:
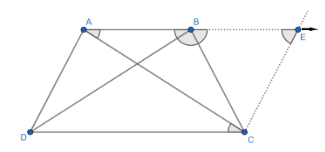
We have trapezium $ABCD$ in which $AB\parallel CD$ and $AD=BC$ .
Construction: Draw a line parallel to $AD$ through $C$ and extend the segment $AB$ to meet the line drawn through $C$ . Let they intersect at a point $E$ .

Now, as it is given that $AB\parallel CD$ so $AE\parallel CD$ and by construction, we can say that $AD\parallel CE$ . Then, $AECD$ is a quadrilateral in which opposite sides are parallel so, $AECD$ will be a parallelogram. Then, $AD=CE$ as opposite sides of the parallelogram are equal.
Now, consider $\Delta BCE$ we can write that, $AD=BC=CE$ . So, the $\Delta BCE$ is an isosceles triangle in which $BC=CE$ . As we know that in an isosceles triangle angles opposite to equal sides of an isosceles triangle are equal. Then,
$\angle CBE=\angle CEB.........\left( 1 \right)$
Now, as by construction $AE\parallel CD$ and $AE$ in the transversal then, interior angles on the same side of the transversal are supplementary angles. Then,
$\begin{align}
& \angle DAB+\angle CEB={{180}^{0}} \\
& \Rightarrow \angle DAB={{180}^{0}}-\angle CEB \\
\end{align}$
Now, using the equation in the above equation. Then,
$\begin{align}
& \angle DAB={{180}^{0}}-\angle CEB \\
& \Rightarrow \angle DAB={{180}^{0}}-\angle CBE...............\left( 2 \right) \\
\end{align}$
Now, as $AE$ is a straight line, so $\angle CBA$ and $\angle CBE$ will be linear pairs. Then,
$\begin{align}
& \angle CBA+\angle CBE={{180}^{0}} \\
& \Rightarrow \angle CBA={{180}^{0}}-\angle CBE............\left( 3 \right) \\
\end{align}$
Now, comparing equation (2) and equation (3). Then,
$\begin{align}
& \angle DAB={{180}^{0}}-\angle CBE=\angle CBA \\
& \Rightarrow \angle DAB=\angle CBA..............\left( 4 \right) \\
\end{align}$
Now, consider $\Delta ABD$ and $\Delta BAC$ . Then,
$\begin{align}
& AB=BA\text{ }\left( common \right) \\
& \angle DAB=\angle CBA\text{ }\left( from\text{ 4} \right) \\
& AD=BC\text{ }\left( Given \right) \\
\end{align}$
Now, by the side angle side congruence rule we can write that $\Delta ABD\cong \Delta BAC$ . And as we know that in a pair of congruent triangles corresponding sides of the triangle are equal. Then, $AD=BC$ .
Thus, we have proved that diagonals of the given trapezium are equal in length.
Hence, proved.
Note: Here, the student must take care of the geometrical properties of the parallelogram. Moreover, be careful in writing the name of congruent triangles. For example in this question we cannot write that $\Delta ADB\cong \Delta BAC$ , the correct way is $\Delta ABD\cong \Delta BAC$ .
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




