Question

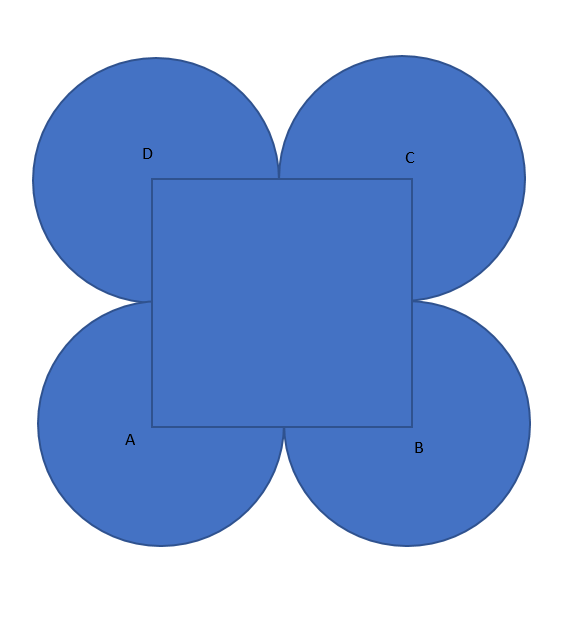
In the given figure, ABCD is a square of side 7 cm and A, B, C and D are the centres of equal circles which touch externally in pairs. The area of the coloured region is

A. $115.5c{m^2}$
B. $164.5c{m^2}$
C. $66.5c{m^2}$
D. $266.5c{m^2}$

Answer 1

Hint: We will observe that we have cut off quadrant from each of the circles. So, we will find the area of the left out circles and the square using the common formulas we have for the area of the circle and the square and then add them up to get the required answer.

Step-By-Step answer:
We are given that A, B, C and D are the centres of the equal circles we have in the figure given above.
So, the square ABCD is covering the quadrants of all the circles. So, 4 times the quadrant means it is covering one circle out of 4.
So, the left part means we have 3 circles, whose area we need to find and add in the area of the square ABCD.
Since, we see that the half of the side of a square is covering up one of the quadrants.
So, the radius of the circle is equal to the half of the side of the square.
$ \Rightarrow $Radius of circle = $\dfrac{7}{2}cm$
We know that area of a circle is given by the following formula:-
$ \Rightarrow $Area of a circle = $\pi {r^2}$, where r is the radius of the circle.
$ \Rightarrow $Area of a circle = $\pi \times {\left( {\dfrac{7}{2}} \right)^2}$
Putting the value of $\pi $ as $\dfrac{{22}}{7}$, we will then obtain:-
$ \Rightarrow $Area of a circle = $\left( {\dfrac{{22}}{7} \times \dfrac{7}{2} \times \dfrac{7}{2}} \right)c{m^2}$
Simplifying the calculations on the right hand side, we will get:-
$ \Rightarrow $Area of a circle = $\left( {11 \times \dfrac{7}{2}} \right)c{m^2}$
Simplifying the calculations on the right hand side further, we will get:-
$ \Rightarrow $Area of a circle = $\dfrac{{77}}{2}c{m^2}$
Since, there are 3 circles whose area we require to find.
$ \Rightarrow $Area of all the circles we require = $\left( {3 \times \dfrac{{77}}{2}} \right)c{m^2}$
Simplifying the calculations on the right hand side, we will get:-
$ \Rightarrow $Area of all the circles we require = $\dfrac{{231}}{2}c{m^2} = 115.5c{m^2}$ …………….(1)
Now, we got to find the area of the square ABCD using the formula that area of a square is given by:-
$ \Rightarrow Area = {\left( {Side} \right)^2}$
$ \Rightarrow Area = {\left( 7 \right)^2} = 49c{m^2}$ ………………..(2)
Adding the equations (1) and (2), we will get:-
$ \Rightarrow $Area of the shaded region = (115.5 + 49) square cm = 164.5 square cm.

$\therefore $ the correct option is (B).

Note: The students must notice that they need to eradicate the area of quadrants because that has been covered up by the square.
The students may also use the formula for the area of sectors and find the area of the sector with an angle of 270 degrees and add it four times to get the area of the shaded region other than square and then find the area of the square as we did above and add them up to get the answer.
The students must commit the following formulas:-
$ \Rightarrow $Area of a square = ${\left( {Side} \right)^2}$
$ \Rightarrow $Area of a circle = $\pi {r^2}$, where r is the radius of the circle.