Question

In the given figure, ABCD is a square, M is the midpoint of AB and $PQ\bot CM$ . Which of the following statements is not true?

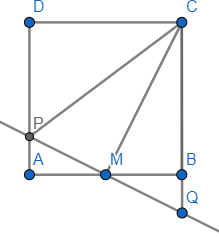
(a) AM=MB
(b) CP=CQ
(c) CP=CB
(d) PM=MQ

Answer 1

Hint: Check the congruency of the triangle PAM and the triangle QBM followed by checking the congruency of the triangle CPM and triangle CQM.

Complete step-by-step answer:
It is given that M is the midpoint of AB, so we can say that AM=MB which is equal to half of the length of AB. Therefore, option (a) is true.
Now in $\Delta PAM\text{ and }\Delta \text{QBM}$ , we have:
AM=BM
$\angle QBM=\angle PAM=90{}^\circ $
And $\angle QMB\text{ and }\angle PMA$ are vertically opposite angles, so they are equal.

So, by ASA criteria, we can say that $\Delta PAM\cong \Delta \text{QBM}$ .
Therefore, by using the corresponding part of congruent triangles (CPCT), we can say that PM=MQ , so option (d) is also true.
Now in $\Delta CPM\text{ and }\Delta C\text{QM}$ , we have:
PM=QM
\[\angle CMQ=\angle CMP=90{}^\circ \]
And CM is common to both the triangles.
So, by SAS criteria, we can say that $\Delta CPM\cong \Delta C\text{QM}$ .
Therefore, by using the corresponding part of congruent triangles (CPCT), we can say that CP=CQ , so option (b) is also true.
Hence, we can conclude that the answer to the above question is option (c).

Note: It is prescribed to learn all the basic theorems related to congruence and similarity of triangles as they are used quite often. Also, learn the properties of parallelograms, including squares, as they might also be needed for solving such problems as we used in the above question.