Question

In the given figure, ABCD is a rhombus. Diagonals AC and BD intersect each other at E.
$\angle 1=50{}^\circ $ then $\angle BCD=$

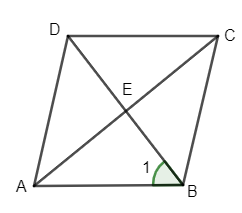
(a)$100{}^\circ $
(b)$90{}^\circ $
(c)$80{}^\circ $
(d)None of these

Answer 1

Hint: Firstly, apply the properties of rhombus to the angle at a given vertex. So, by that we can say the total angle made at vertex from the rule of adjacent angles are supplementary. Find the angle which is required in the question.

Complete step-by-step answer:
Rule-1: Diagonals bisect each other. Thereby, bisect the angle at vertex.
Rule-2: Adjacent angles are supplementary.
Proof of diagonals bisect the angles.
By definition, we know rhombus is a parallelogram. So, we take properties of parallel lines and their corresponding angles into consideration.
By figure we can say each diagonal divides the shape into 2 triangles. So, we can use the triangles congruence properties also.
We must also take the isosceles triangle and their properties into consideration.
We prove for the diagonal AC and we take BD granted as a similar way can be used from BD.
By saying the general condition in rhombus all sides are equal, we can say:
Line segment DA is congruent to line segment AB.
Line segment CD is congruent to line segment CB.
The line segment CA is the same in both. So, it is congruent to itself.
By SSS axiom we say triangle CAD and triangle BAC are congruent. By this we can say angles BAC and CAD are congruent.
Using this to our question $\angle ABC=\angle ABD+\angle DBC$ as the angles ABD and DBC are equal and their value is given 50. By substituting this, we get:
$\angle ABC=100{}^\circ $ …..........................(1)
We know adjacent angles in rhombus are supplementary. By this we can say, the sum of adjacent angles is $180{}^\circ $. We get $\angle ABC+\angle BCD=180$ . By equation (1), we get:
$\angle BCD=180-100=80{}^\circ $
Therefore, $80{}^\circ $ is the required value. Option (c) is correct.

Note: (1) Proof of diagonals bisecting the angles is important. We must have the knowledge of finding congruent triangles from any geometry because almost all proofs in geometry use concepts of congruence and similarity.
(2) Always remember adjacent angles must sum to a total of $180{}^\circ $.
(3) Alternate method is to take the opposite angles to be equal. Assume unknown angle as x. Now equate the sum of 4 angles to $360{}^\circ $ .