Question

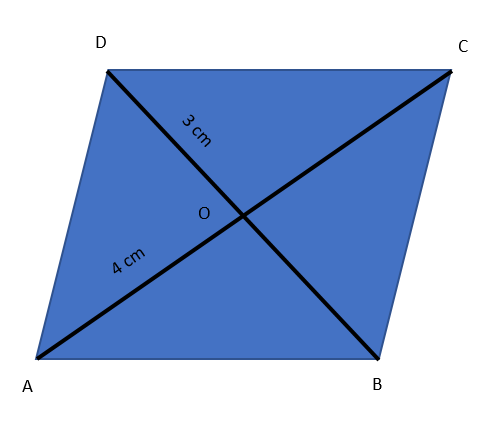
In the given figure, ABCD is a rhombus, AO = 4 cm and DO = 3 cm. Then, find the perimeter of the rhombus.

Answer 1

Hint: We will first make use of the fact that the diagonals of a rhombus bisect each other at right angles. Then, we get a right angled triangle and thus on using the Pythagorean Theorem, we get the required answer.

Step-By-Step answer:
We are given that we have a rhombus ABCD.
We are also given that AO = 4 cm and DO = 3 cm.
Now, we also know that the diagonals of a rhombus bisect each other at right angles.
Therefore the angles corresponding to O that is angle AOD, AOB and so on are all right angles.
Now, we have got that $\angle AOD = {90^ \circ }$.
Now, consider the $\vartriangle AOD$:-
We have $A{D^2} = A{O^2} + D{O^2}$ (By Pythagorean Theorem)
[Pythagorean Theorem states that the sum of square of non – hypotenuse sides is equal to the square of the hypotenuse]
Now, we are already given the lengths of AO and DO.
$ \Rightarrow A{D^2} = {4^2} + {3^2}$
Solving the squares of the values in right hand side, we will get:-
$ \Rightarrow A{D^2} = 16 + 9$
Simplifying the values on the right hand side, we will then obtain:-
$ \Rightarrow A{D^2} = 25$
$ \Rightarrow AD = \pm 5$
Since, the length cannot be in negative terms, we then get:-
$ \Rightarrow AD = 5$
Now, since we know that the sides of a rhombus are all equal.
Therefore, AB = BC = CD = AD.
Therefore, all the sides are 5 cm each.
Perimeter of a rhombus is 4 times side length which can be written as:-
$ \Rightarrow $ Perimeter = $4 \times Side$
Putting the values of the side length we just obtained as 5 cm.
$ \Rightarrow $ Perimeter = $4 \times 5$cm
Simplifying the calculations on the right hand side, we then obtain:-
$ \Rightarrow $ Perimeter = 20 cm

Hence, the answer is 20 cm.

Note: The students must know that Perimeter is basically the total length of the sides. Here, in the rhombus ABCD, the perimeter is actually the sum of all sides AB, BC, CD and AD but since they are all equal in length, we get 4 times the side length.
 Because Perimeter = AB + BC + CD + DA
(Since AB = BC = CD = AD)
$ \Rightarrow $Perimeter = AD + AD + AD + AD = $4 \times AD$
Hence, proved.