Question

In the given figure $ABCD$ is a quadrilateral in which $P$, $Q$, $R$ and $S$ are mid-points the sides $AB$, $BC$, $CD$ and $DA$. $AC$ is a diagonal. Show that:
$SR\;\parallel AC$ and $SR = \dfrac{1}{2}AC$

Answer 1

Hint: In the solution we will use the Midpoint theorem. The theorem says that When line segments attach the mid-points of any two sides of a triangle, then that line segments are parallel to the other side.


Complete Step-by-step Solution
Given:
$ABCD$ is a quadrilateral in which $P$, $Q$, $R$ and $S$ are the mid-points of the sides $AB$, $BC$, $CD$ and $DA$ respectively.

The following is the schematic diagram of the quadrilateral $ABCD$.
  

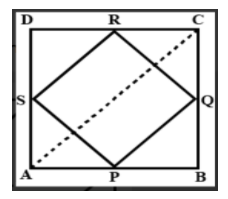
To prove that
$SR\;\parallel AC$ and $SR = \dfrac{1}{2}AC$
In the triangle $\Delta DAC$, the point $S$ is the midpoint of $DA$ whereas $R$ is the midpoint of $DC$.
According to the mid-point theorem, SR will be parallel to the diagonal of the quadrilateral that is AC.
$SR\parallel AC$
Therefore, it is proved that $SR\parallel AC$.
Since, we know that from the mid-point theorem that the line connecting the mid-points of two sides of the triangle will be parallel to the other side and also half of it. Then with the help of mid-point theorem, we get the required relation,
 $SR = \dfrac{1}{2}AC$


Note: In this problem, make sure to use the mid-point theorem instead of other theorems when any question is asking about a quadrilateral with midpoints. The solution is totally based on the mid-point theorem. Mid-point is the point on the line segment which is exactly at the middle and it is equidistant from the end point of the line segment.