
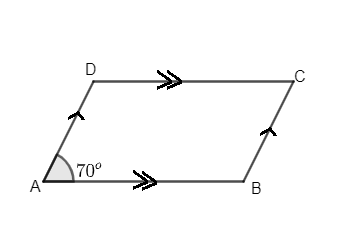
In the given figure, ABCD is a parallelogram in which $\angle A={{70}^{\circ }}$ .Calculate $\angle B,\angle C$ and $\angle D$

Answer
614.1k+ views
Hint: Use the properties of angles of parallelogram which are opposite angles are equal and also adjacent angles are supplementary to each other.
Complete step-by-step answer:
In the question as figure is given,
We are given a parallelogram ABCD such that angle A is ${{70}^{\circ }}$
Now we will first note that what are the properties of parallelogram,
(i) Opposite angles are equal
(ii) Opposite sides are equal and parallel
(iii) Sum of adjacent angles is ${{180}^{\circ }}$ or we can also say that adjacent angles are supplementary to each other.
Now as in the question it is given that angle A is \[{{70}^{\circ }}\] so as we know that opposite angles of parallelogram is equal is it’s property so angle C = angle A so, angle C is ${{70}^{\circ }}$ .
Now as we know angle A is ${{70}^{\circ }}$ so angle B can be find out using fact that angle A and angle B is supplementary to each other.
Hence, we can say that angle A + angle B = ${{180}^{\circ }}$
So, angle B is equal to ${{180}^{\circ }}$ - angle A which is equal to 180 – 70 = 110
Hence the value of angle B is ${{110}^{\circ }}$
Again we will use the property that opposite angles are equal so as we know that angle B is ${{110}^{\circ }}$ so angle D is equal to angle B, so the angle D is ${{110}^{\circ }}$ .
Hence the value of angle D is ${{110}^{\circ }}$ .
Note: Students should know about the properties of angle related to the parallelogram.
Complete step-by-step answer:
In the question as figure is given,

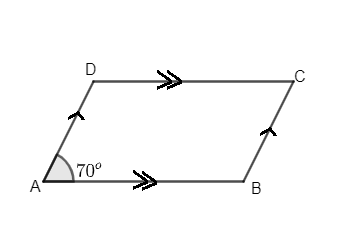
We are given a parallelogram ABCD such that angle A is ${{70}^{\circ }}$
Now we will first note that what are the properties of parallelogram,
(i) Opposite angles are equal
(ii) Opposite sides are equal and parallel
(iii) Sum of adjacent angles is ${{180}^{\circ }}$ or we can also say that adjacent angles are supplementary to each other.
Now as in the question it is given that angle A is \[{{70}^{\circ }}\] so as we know that opposite angles of parallelogram is equal is it’s property so angle C = angle A so, angle C is ${{70}^{\circ }}$ .
Now as we know angle A is ${{70}^{\circ }}$ so angle B can be find out using fact that angle A and angle B is supplementary to each other.
Hence, we can say that angle A + angle B = ${{180}^{\circ }}$
So, angle B is equal to ${{180}^{\circ }}$ - angle A which is equal to 180 – 70 = 110
Hence the value of angle B is ${{110}^{\circ }}$
Again we will use the property that opposite angles are equal so as we know that angle B is ${{110}^{\circ }}$ so angle D is equal to angle B, so the angle D is ${{110}^{\circ }}$ .
Hence the value of angle D is ${{110}^{\circ }}$ .
Note: Students should know about the properties of angle related to the parallelogram.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





