Question

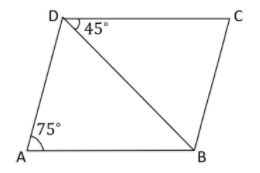
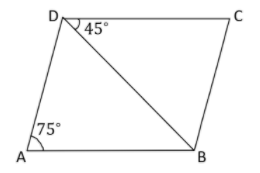
In the given figure, ABCD is a parallelogram in which $\angle BDC = {45^ \circ }$ and $\angle BAD = {75^ \circ }$.Then $\angle CBD = $?
          

A)${150^ \circ }$
B)${105^ \circ }$
C)${60^ \circ }$
D)${75^ \circ }$

Answer 1

Hint: You should know the properties of parallelogram that opposite sides are parallel and equal and also opposite angles are equal and sum of adjacent angles is ${180^ \circ }$. Apply these properties you will get the answer.

Complete step-by-step answer:
So, basically, we are given a parallelogram ABCD and $\angle BDC = {45^ \circ }$ and $\angle BAD = {75^ \circ }$ are given and we need to find $\angle CBD$.

Now, as we know that ABCD is a parallelogram and we know the properties of parallelogram, it has both opposite sides parallel and equal.
Here, ABCD is a parallelogram and it has both opposite sides parallel and equal.

          

Therefore,
$
  AD||BC \\
  AD = BC \\
 $
Also,
$
  AB||DC \\
  AB = DC \\
 $
Now, we also know that opposite angles of parallelograms are equal.
So,
$
  \angle DAB = \angle BCD \\
  \angle BCD = {75^ \circ } \\
 $
Now, we assume that $\angle CBD = {x^ \circ }$
So, we know that between two parallel lines two alternate angles are equal.
Therefore,
Here, $CD||AB$
Hence, $\angle BDC = \angle ABD$
Because both are alternate interior angles between parallel lines.
So, $\angle ABD = {45^ \circ }$
Also, we know $AD||BC$
Hence, $\angle ADB = \angle CBD$
Because both are alternate interior angles.
So, $\angle CBD = {x^ \circ }$
So, $\angle ADB = {x^ \circ }$
Now we know that sum of the angles of the quadrilateral is ${360^ \circ }$ (1)
Here from above parallelogram, we know that
$
  \angle A = {75^ \circ } \\
  \angle B = \angle ABD + \angle CBD = 45 + x \\
  \angle C = {75^ \circ } \\
  \angle D = \angle ADB + \angle BDC = x + 45 \\
 $
Now putting all angle values in equation (1)
$
  \angle A + \angle B + \angle C + \angle D = 360 \\
  75 + \left( {45 + x} \right) + 75 + \left( {x + 45} \right) = 360 \\
  240 + 2x = 360 \\
  2x = 120 \\
  x = {60^ \circ } \\
 $

So, the correct answer is “Option C”.

Note: As we know that $\angle A = \angle C$ because opposite angles of parallelogram are equal. And then we can solve for triangle CBD in which two angles are given. We can find the third side as we know that the sum of angles of the triangle is ${180^ \circ }$. You can use this method to save your time.