Question

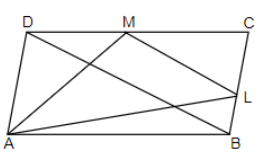
In the given figure, ABCD is a parallelogram. If L and M are the mid-points of the sides BC and CD respectively, then prove that $8\left( Area\text{ }\Delta ALM \right)=3\left( Area\text{ }ABCD \right)$.

Answer 1

Hint: We will use the mid-point theorem according to which the line joining the mid-points of two sides of a triangle is parallel to the third side and it is equal to half the length of the third side.

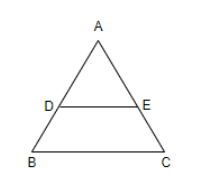
In the triangle ABC, we have D and E as the mid-points of side AB and AC respectively. So, according to the mid-point theorem, $DE\parallel BC$ and $DE=\dfrac{1}{2}BC$ as area of $\Delta ADE=\dfrac{1}{4}$ area of $\Delta ABC$ . We will find the area of $\Delta DAM,\Delta ABL,\Delta MLC$ and subtract it from the area of the parallelogram ABCD. We get the area $\Delta XYA=\dfrac{3}{8}$ area of parallelogram ABCD and then we will solve accordingly.

Complete step-by-step answer:
It is given in the question that ABCD is a parallelogram, L and M are the mid-points of the sides BC and CD respectively, and we have to prove that $8\left( Area\text{ }\Delta ALM \right)=3\left( Area\text{ }ABCD \right)$.

We know that according to the mid-point theorem, the line joining the mid-points of two sides of a triangle is parallel to the third side and is equal to half the length of the third side. So, in triangle DBC, we have L and M as the mid-points of sides CB and CD respectively. So, it means that LM is parallel to DB and $LM=\dfrac{1}{2}DB$. Now, let us assume that the height of the below given triangle, DBC is h.

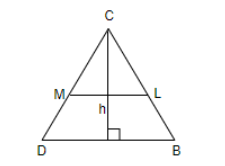
Also, we know that in triangle DBC, the line segment LM divides the height also into $\dfrac{h}{2}$. We know that the area of a triangle is given as, $\dfrac{1}{2}\times base\times height$. So,
The area of $\Delta DBC=\dfrac{1}{2}\times DB\times h\Rightarrow \dfrac{DBh}{2}$.
Also, the area of $\Delta MLC=\dfrac{1}{2}\times ML\times \dfrac{h}{2}$.
Now, we know that, $ML=\dfrac{1}{2}DB$, so we will substitute this in the above equality. So, we get,
The area of $\Delta MLC=\dfrac{1}{2}\times \dfrac{DB}{2}\times \dfrac{h}{2}\Rightarrow \dfrac{DBh}{8}$.
So, on comparing the area of $\Delta DBC$ with the area of $\Delta MLC$, we get,
$\begin{align}
  & \dfrac{DBh}{2}=\dfrac{DBh}{8} \\
 & \Rightarrow 4DBh=DBh \\
 & \Rightarrow \dfrac{1}{4}\left( area\text{ }of\text{ }\Delta DBC \right)=area\text{ }of\text{ }\Delta MLC \\
\end{align}$
We also know that the diagonals of a parallelogram divides it into two equal triangles, so we get,
Area of $\Delta MLC=\dfrac{1}{8}$area of parallelogram ABCD.
Now, in $\Delta ABD$ and $\Delta ABL$, we have,
Area of $\Delta ABD=\dfrac{1}{2}\times AB\times DA$
And the area of $\Delta ABL=\dfrac{1}{2}\times AB\times BL$.
Now, we know that $BL=\dfrac{1}{2}DA$, so, we can say that,
$\Rightarrow \dfrac{1}{2}\left( area\text{ }of\text{ }\Delta ABC \right)=area\text{ }of\text{ }\Delta DBL$.
And we have the area of the parallelogram ABCD = 4 area of triangle DBL. Or we can say that,
Area of $\Delta DBL=\dfrac{1}{4}$ area of parallelogram ABCD.
Similarly, in $\Delta ACD$ and $\Delta ADM$, we will have,
Area of $\Delta ACD$ = 2 area of $\Delta ADM$.
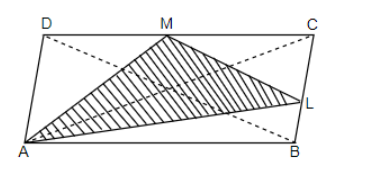
So, now, we can calculate the area of $\Delta ALM$ by subtracting the area of $\Delta MLC,\Delta ABL,\Delta ADM$ from the area of the parallelogram ABCD. So, we get,
\[\begin{align}
  & \text{Area }\Delta ALM=\left( \text{area parallelogram }ABCD \right)-\left[ \left( \text{area }\Delta MLC \right)+\left( \text{area }\Delta ABL \right)+\left( \text{area }\Delta ADM \right) \right] \\
 & \Rightarrow \text{area }ABCD-\left[ \dfrac{1}{8}\left( \text{area }ABCD \right)+\dfrac{1}{4}\left( \text{area }ABCD \right)+\dfrac{1}{4}\left( \text{area }ABCD \right) \right] \\
 & \Rightarrow \text{area }ABCD-\left[ \dfrac{1+2+2}{8} \right]\text{area }ABCD \\
 & \Rightarrow \text{area }ABCD-\dfrac{5}{8}\text{area }ABCD \\
 & \Rightarrow \left( \dfrac{8-5}{8} \right)\text{area }ABCD \\
 & \Rightarrow \dfrac{3}{8}\text{area }ABCD \\
\end{align}\]
So, we get the area of $\Delta ALM=\dfrac{3}{8}$ area of parallelogram ABCD. On multiplying both sides with 8, we get,
$8\left( Area\text{ }\Delta ALM \right)=3\left( Area\text{ }ABCD \right)$.
Hence it is proved.

Note: Many students make mistakes by directly trying to find the area of $\Delta ALM$ and as a result they get stuck initially as there is no direct method to find the area of triangle AYX in a parallelogram. One should also be careful while calculating the areas of the individual triangles.