Question

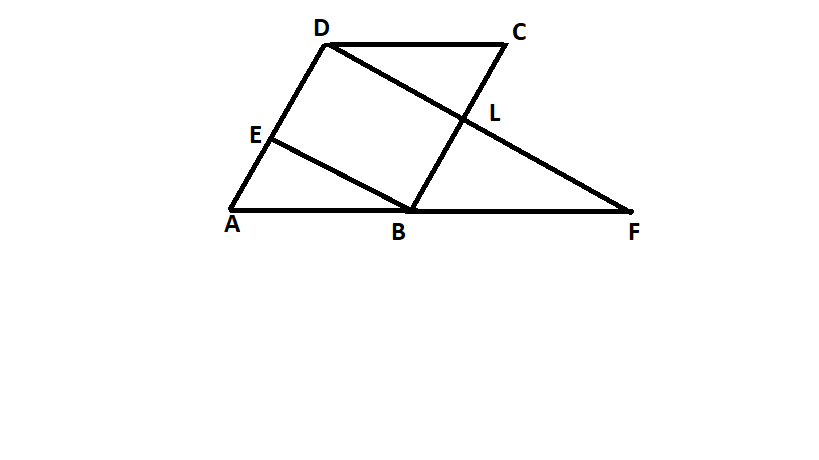
In the given figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that:
${\text{(i)}}{\text{.}}$$AF = 2DC$
${\text{(ii)}}{\text{.}}$ $DF = 2DL$

Answer 1

Hint – Given, E is the midpoint of AD and also EB||DL. So, we can also say by Mid-point Theorem that- B is also the mid-point of AF. Hence, $AF = 2AB$. Use these concepts to solve further.

Complete step-by-step answer:
According to the question, it is given that-
ABCD is a parallelogram and E is the mid-point of AD and also EB||DF.
Now, since E is the midpoint of AD and also EB||DF, by using mid-point theorem we can say that,
B is also the mid-point of AF, which implies that $AF = 2AB \to (1)$
Since, ABCD is a parallelogram, we can say that-
$CD = AB$, this means that we can also write equation (1) as-
$AF = 2CD$.
Hence, (i) $AF = 2CD$ is proved.
Now, also EB||DL and ED||BL, (as E is the mid point drawn parallel to EB), which implies that EBLD is a parallelogram-
$\therefore BL = ED = \dfrac{1}{2}AD = \dfrac{1}{2}BC = CL$
Now, in triangles DCL and FBL, we have
$CL = BL$ (Proved above)
$\angle DLC = \angle FLB$ (vertically opposite angles)
$\angle CDL = \angle BFL$ (Alternate angles)
$\therefore \vartriangle DCL \cong \vartriangle FBL$ (By AAS congruence criterion)
$\therefore DC = BF$ and $DL = FL$
Since, DL = FL, we can say that L is the midpoint of DF, which shows that $DF = 2DL$.
Therefore, (ii) $DF = 2DL$ is proved.

Note- Whenever such types of questions appear then always use the properties of the given figure, as in this question ABCD is a parallelogram, so using the properties like opposite sides of a parallelogram are parallel, we can conclude many results. Also, we have used the mid-point theorem to prove certain results.