Question

In the given figure, ABCD is a parallelogram, and X and Y are points such that DX = BY. Prove that

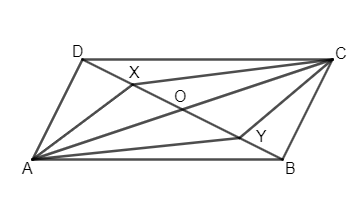
(a) AXCY is a parallelogram
(b) AX = XY, AY = CX
(c) $\Delta AYB\cong \Delta CXD$
(d) $\Delta AXD\cong \Delta CYB$

Answer 1

Hint: Draw a suitable diagram with the help of the given information to visualize the problem in a right way. Use the property: “if diagonals of any quadrilateral is bisecting each other, then it will be a parallelogram. Opposite sides of a parallelogram are equal and parallel to each other, use these properties to solve the problem.

Complete step-by-step answer:
Here, we are given a parallelogram ABCD, such that points X and Y are lying on BD in a way that DX = BY. So, we know
$DX=BY.........\left( i \right)$
As we know the property of parallelogram suggests that opposite sides and opposite angles are equal to each other and the diagonals of the parallelogram bisect each other. So, we get
$\begin{align}
  & OD=OB.......\left( ii \right) \\
 & OC=OA........\left( iii \right) \\
\end{align}$

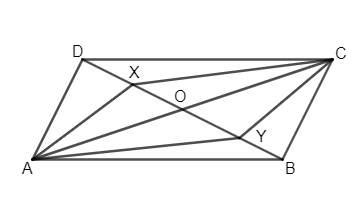
Now from equation (iii) we have
OD = OB
Subtract BY from both sides of the above equation, we get
OD – BY = OB – BY
Now, we can replace BY of L.H.S. sides of the above equation by DX from the equation (i). So, we get
OD – DX = OB – BY
Now, we can observe the length OD – DX will be equal to OX and OB – BY will be equal to OY. So, we get
OX = OY ………………(iv)
Now, in quadrilateral AXCY, we get
OX = OY and OA = OC …………..(v)
As XY and AC are the diagonals of the quadrilateral AXCY and they are getting bisected at point O from the equation.
So, as we know any quadrilateral will be a parallelogram, if its diagonals are getting bisected. So, we get that AXCY will represent a parallelogram because their diagonals are getting bisected.
Hence part(a) of the question is proved.
Now, as AXCY is representing a parallelogram, it will follow all the properties of the parallelogram. Hence as we know parallelogram has equal opposite sides. It means we can write equations from parallelogram AXCY as
AX = CY, AY = CX
Hence part (b) is proved.
In $\Delta AYB$ and $\Delta CXD$, we have
AB = CD (ABCD is a parallelogram)
AY = CX (AXCY is a parallelogram)
DX = BY (Given)
Hence, by SSS criteria of congruence of triangles, $\Delta AYB$ will be congruent to $\Delta CXD$ i..e. $\Delta AYB\cong \Delta CXD$ .
So, part (c) of the question is proved
Similarly, in $\Delta AXD$ and $\Delta CYB$ , we have
AD = BC (ABCD is a parallelogram)
AX = CY (AXCY is a parallelogram)
DX = BY (Given)
Hence, by SSS criteria triangles AXD and CYB are congruent to each other i.e. $\Delta AXD\cong \Delta CYB$
So, part(d) of the question is proved.

Note: Draw a suitable diagram with the given information for the perfect visualization of the problem.
One needs to be clear with the properties of a parallelogram. One may not be able to solve these kinds of questions without knowing properties of the given shape as we can not do any mathematical calculations with these kinds of problems (proving). So, be clear with the concepts and theorems for these types of questions in future.