Question

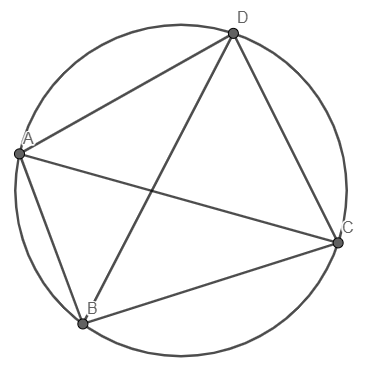
In the given figure $ABCD$ is a cyclic quadrilateral in which $AC$ and $BD$ are its diagonals. If $\angle DBC={{55}^{\circ }}$ and $\angle BAC={{45}^{\circ }}$, find $\angle BCD$.

Answer 1

Hint: In this question we have been given with a cyclic coordinate $ABCD$. A cyclic quadrilateral is a quadrilateral which has all its edges inside a circle. We have to find the value of $\angle BCD$ given the values of $\angle DBC={{55}^{\circ }}$ and $\angle BAC={{45}^{\circ }}$. We will solve this question by using the properties of a cyclic quadrilateral that the angles in the same segment are always equal and the opposite angles of a cyclic quadrilateral have a sum of ${{180}^{\circ }}$.

Complete step by step solution:
We have the cyclic quadrilateral given as $ABCD$.
We know the property that the angles in the same segment of a cyclic quadrilateral are the same therefore, we can write:
$\Rightarrow \angle CAD=\angle DBC={{55}^{\circ }}$
Now we can see from the diagram that $\angle DAB=\angle CAD+\angle BAC$ and we have the value of $\angle BAC={{45}^{\circ }}$.
On substituting the values, we get:
$\Rightarrow \angle DAB={{55}^{\circ }}+{{45}^{\circ }}$
On adding, we get:
$\Rightarrow \angle DAB={{100}^{\circ }}$
Now since the opposite angles of a cyclic quadrilateral are always the same, we can say that:
$\Rightarrow \angle DAB+\angle BCD={{180}^{\circ }}$
On rearranging the expression, we get:
$\Rightarrow \angle BCD={{180}^{\circ }}-\angle DAB$
On substituting the value of $\angle DAB={{100}^{\circ }}$, we get:
$\Rightarrow \angle BCD={{180}^{\circ }}-{{100}^{\circ }}$
On simplifying, we get:
$\Rightarrow \angle BCD={{80}^{\circ }}$, which is the required solution.

Note: It is to be remembered that a cyclic quadrilateral is an inscribed figure. An inscribed figure is a figure which fits inside another shape. In this case it is a cyclic quadrilateral that fits inside a circle. There can also be other inscribed shapes such as a triangle or a polygon inside a circle. The various properties of shapes should be remembered while doing these types of sums.