
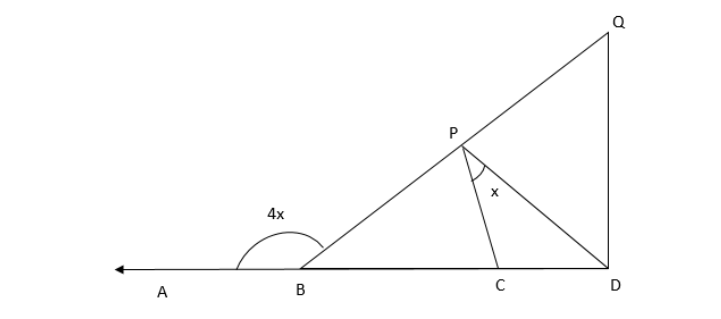
In the given figure, $ ABCD $ and $ BPQ $ are straight lines. If $ BP = BC $ and $ DQ $ is parallel to $ CP $ , prove that
(i) $ CP = CD $
(ii) $ DP $ bisects $ \angle CDQ $

Answer
576k+ views
Hint: In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
Complete step-by-step answer:
Observe the following figure.
It is given in the figure,
Exterior angle $ PBA = 4x. $
To prove,
$ CP = CD $
Now,
$ \angle BPC = \angle PCB $ . . . . (from the figure)
We know that an exterior angle is equal to the sum of two opposite interior angles.
Therefore, $ \angle BPC + \angle PCB = 4x $
Clearly interior angle $ BPC $ and angle $ PCB $ are equal.
Then,
$ 2\angle BPC = 4x $
On dividing by $ 2 $ in the above equation with both side and we get,
$ \angle BPC = 4x $
$ \Rightarrow \angle BPC = \angle PCB = 2x $
Now, $ DQ\parallel CP $ . . . (Given)
$ \angle QDC = \angle PCB $ . . . (Corresponding angle property)
$ \Rightarrow \angle QDC = 2x $
We know that an exterior angle is equal to the sum of two opposite interior angles.
$ \Rightarrow \angle PCB = \angle CPD + \angle PDC $
$ \Rightarrow 2x = x + \angle PDC $
On rearranging the above equation, we get,
$ \Rightarrow \angle PDC = x $
As $ \angle QDC = 2x $ and $ \angle PDC = x $
Hence, it is proven that $ DP $ bisects $ \angle CDQ $ from the above solution.
And we have,
$ \angle PD = x $ and $ \angle CPD $
Since sides opposite to equal angles are equal,
Hence, $ CP = CD $ (Hence prove)
Note: An exterior angle of a triangle is equal to the sum of the opposite interior angles. For more on this see Triangle external angle theorem. If the equivalent angle is taken at each vertex, the exterior angles always add to 360° In fact, this is true for any convex polygon, not just triangles.
Complete step-by-step answer:
Observe the following figure.

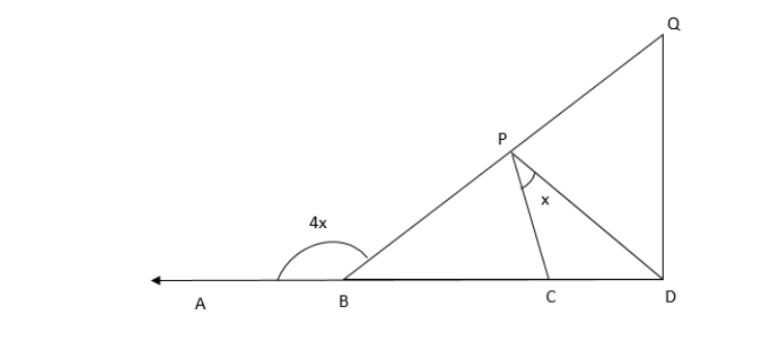
It is given in the figure,
Exterior angle $ PBA = 4x. $
To prove,
$ CP = CD $
Now,
$ \angle BPC = \angle PCB $ . . . . (from the figure)
We know that an exterior angle is equal to the sum of two opposite interior angles.
Therefore, $ \angle BPC + \angle PCB = 4x $
Clearly interior angle $ BPC $ and angle $ PCB $ are equal.
Then,
$ 2\angle BPC = 4x $
On dividing by $ 2 $ in the above equation with both side and we get,
$ \angle BPC = 4x $
$ \Rightarrow \angle BPC = \angle PCB = 2x $
Now, $ DQ\parallel CP $ . . . (Given)
$ \angle QDC = \angle PCB $ . . . (Corresponding angle property)
$ \Rightarrow \angle QDC = 2x $
We know that an exterior angle is equal to the sum of two opposite interior angles.
$ \Rightarrow \angle PCB = \angle CPD + \angle PDC $
$ \Rightarrow 2x = x + \angle PDC $
On rearranging the above equation, we get,
$ \Rightarrow \angle PDC = x $
As $ \angle QDC = 2x $ and $ \angle PDC = x $
Hence, it is proven that $ DP $ bisects $ \angle CDQ $ from the above solution.
And we have,
$ \angle PD = x $ and $ \angle CPD $
Since sides opposite to equal angles are equal,
Hence, $ CP = CD $ (Hence prove)
Note: An exterior angle of a triangle is equal to the sum of the opposite interior angles. For more on this see Triangle external angle theorem. If the equivalent angle is taken at each vertex, the exterior angles always add to 360° In fact, this is true for any convex polygon, not just triangles.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




