Question

In the given figure, ABC is a quadrant of a circle of radius $ 14cm $ and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Answer 1

Hint: In the question, we are given a figure in which a portion of the figure is shaded with blue color. We are required to find the area of the shaded region with the help of analytical skills. We have to employ the formulae of area of circle and semicircle in order to find the area of the shaded region. We can also use the inclusion exclusion principle in order to find the area of the required portion.

Complete step by step solution:

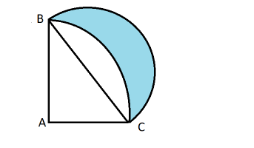
In the question, we are given that the radius of the quadrant is $ 14\;cm $ . So,
$ AB = AC = 14\;cm $ .
So, the area of triangle ABC
$ = \dfrac{{\left( {b \times h} \right)}}{2} = \dfrac{{\left( {14 \times 14} \right)}}{2} = 98\,c{m^2} $
Area of a quadrant of circle $ = \dfrac{{\pi {r^2}}}{4} = \dfrac{1}{4} \times \dfrac{{22}}{7} \times 14 \times 14 $
 $ \Rightarrow 11 \times 14 $
 $ \Rightarrow 154\,c{m^2} $
Using Pythagoras theorem, we know that $ {\left( {Hypotenuse} \right)^2} = {\left( {Altitude} \right)^2} + {\left( {Base} \right)^2} $ . Applying Pythagoras theorem in $ \Delta ABC $ , we get,
 $ \Rightarrow {\left( {BC} \right)^2} = {\left( {AB} \right)^2} + {\left( {AC} \right)^2} $
 $ \Rightarrow {\left( {BC} \right)^2} = {\left( {14} \right)^2} + {\left( {14} \right)^2} $
Calculating the squares and simplifying further, we get,
 $ \Rightarrow {\left( {BC} \right)^2} = 196 + 196 $
 $ \Rightarrow {\left( {BC} \right)^2} = 392 $
 $ \Rightarrow BC = \sqrt {392} $
Simplifying the square root,
 $ \Rightarrow BC = 14\sqrt 2 \,cm $
So, the length of hypotenuse of the right angled triangle is $ 14\sqrt 2 \,cm $ .
So, Diameter of the semicircle $ = 14\sqrt 2 \,cm $
So, the radius of the semicircle is $ 7\,cm $ .
Now, the area of semicircle $ = \dfrac{{\pi {r^2}}}{2} = \dfrac{1}{2} \times \dfrac{{22}}{7} \times 7 \times 7 $
 $ \Rightarrow 11 \times 7 $
 $ \Rightarrow 77\,c{m^2} $
Hence, area of shaded region $ = \,\left( {Area\,of\,Semicircle} \right)\, + \,\left( {Area\,of\,\Delta ABC} \right)\, - \,\left( {Area\,of\,quadrant} \right) $
 $ \Rightarrow \,\left( {77\,c{m^2}} \right)\, + \,\left( {98\,c{m^2}} \right)\, - \,\left( {154\,c{m^2}} \right) $
 $ \Rightarrow \,21\,c{m^2} $
So, the area of the shaded region is $ \,21\,c{m^2} $ .
So, the correct answer is “ $ \,21\,c{m^2} $ ”.

Note: Such problems that require us to find the area of figures relating circles, triangles and any other shape can be solved easily using analytical, logical and critical thinking along with the use of appropriate formulae for finding the area of the shapes in the figure given to us.