Question

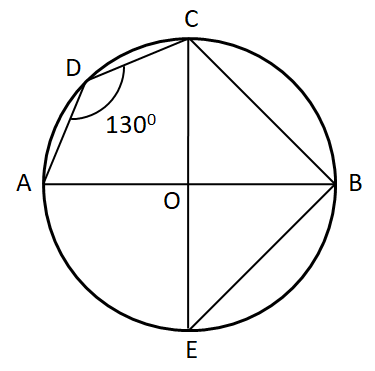
In the given figure, AB is a diameter of the circle with centre O. If angle ADC $={{130}^{\circ }}$ and chord BC$=$ chord BE, find the angle CBE.

Answer 1

Hint: In the given figure, the points A, B, C and D together form a cyclic quadrilateral. We know that the sum of the opposite angles of the cyclic quadrilateral is equal to ${{180}^{\circ }}$ so that \[\angle ABC+\angle ADC={{180}^{\circ }}\]. On substituting the given value $\angle ADC={{130}^{\circ }}$, we will get the value of \[\angle ABC\]. Then, from the given condition chord BC$=$ chord BE, we can show the triangles ODC and ODE to be congruent. Then using CPCT, we will get the final value of the angle CBE.

Complete step by step solution:
In the figure given in the above question, we can see that the points A, B, C and D all lie on the circumference of the given circle. Therefore, the quadrilateral ABCD will be a cyclic quadrilateral.
Now, we know that the sum of the opposite angles of a cyclic quadrilateral is equal to ${{180}^{\circ }}$. Therefore we can write
$\Rightarrow \angle ABC+\angle ADC={{180}^{\circ }}$
Now, according to the question we have $\angle ADC={{130}^{\circ }}$. Substituting this above we get
\[\begin{align}
  & \Rightarrow \angle ABC+{{130}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle ABC={{50}^{\circ }}.......\left( i \right) \\
\end{align}\]
Now, in the triangles OBC and OBE we have
$\Rightarrow BC=BE$ (given)
$\Rightarrow OC=OE$ (radii)
And
\[\Rightarrow OB=OB\] (common)
Therefore, using SSS congruence, we can say that $\Delta OBC\cong \Delta OBE$. Therefore, by CPCT we have
$\begin{align}
  & \Rightarrow \angle OBE=\angle OBC \\
 & \Rightarrow \angle OBE=\angle ABC......\left( ii \right) \\
\end{align}$
Also, from the given figure we can write
$\Rightarrow \angle CBE=\angle OBE+\angle ABC$
Substituting (ii) in the above equation, we get
$\begin{align}
  & \Rightarrow \angle CBE=\angle ABC+\angle ABC \\
 & \Rightarrow \angle CBE=2\angle ABC \\
\end{align}$
Substituting (i) we get
$\begin{align}
  & \Rightarrow \angle CBE=2\left( {{50}^{\circ }} \right) \\
 & \Rightarrow \angle CBE={{100}^{\circ }} \\
\end{align}$
Hence, the value of the angle CBE is equal to ${{100}^{\circ }}$.

Note: We must be familiar with all the types of the congruency of the triangles. There are only five types of the congruency, which are SSS, ASA, AAS, SAS, and RHS. While obtaining the congruence between two triangles, we must take proper care of the order of their labeling.