Question

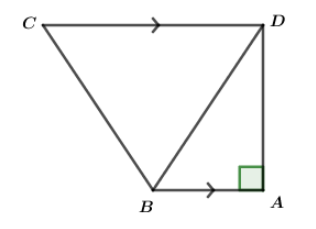
In the given figure, AB || CD, AB = 7 cm, BD = 25 cm and CD = 17 cm. Find the length of side BC.

Answer 1

Hint:Here, we will use Pythagoras theorem and will draw a perpendicular from B on the side CD, named it as E, so that we could get a right angled triangle containing a side BC. Then from triangle BEC, we will find the value of BC.

Complete step-by-step answer:
Here, we are given
ABCD is a trapezium such that$AB||CD$, $\angle DAB = {90^0},AB = 7$cm, $BD = 25$cm and CD =17 cm
In \[\vartriangle ABD,\angle A = {90^0}\]
By Pythagoras theorem, we know that in a right angled triangle the square of the side opposite to the right angle is equal to the sum of squares of the other two sides.
Thus, $B{D^2} = A{B^2} + A{D^2}$
     $ \Rightarrow {25^2} = {7^2} + A{D^2}$
      $\therefore A{D^2} = 576 \Rightarrow AD = 24$
Now, we draw perpendicular BE from B on side CD.

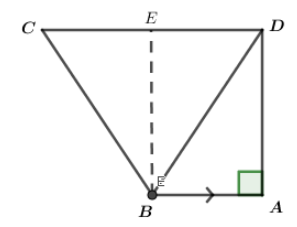
Thus, we get a rectangle ABDE in which AB = ED =7 cm, AD =BE = 24 cm
Therefore, CE = CD – ED = (17- 7) cm = 10 cm
Now in right angled$\vartriangle BCE$, using Pythagoras theorem we have
$B{C^2} = B{E^2} + C{E^2} = {24^2} + {10^2} = 676$
$\therefore BC = 26$cm
Therefore, the length of side BC is 26 cm.

Note:Pythagoras theorem states that
In a right angled triangle the square of the side opposite to the right angle is equal to the sum of squares of the other two sides.
If ABC be a right angle such that angle B = 90°.
Then, AB² + BC² = AC².
It should be noted the side opposite to the right angle in a right angled triangle is called hypotenuse and it is the longest side.
A Pythagorean triplet is the set of three numbers such that the square of the largest number is equal to some of the other two smaller numbers.
Examples: (3, 4, 5); (6, 8, 10) etc.