Question

In the given figure AB, BC and CD are equal chords of a circle with centre O and AD is a diameter. If \[\angle DEF = {110^ \circ }\]. Find \[\angle AEF\] and \[\angle FAB\]

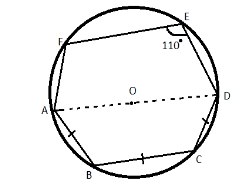
Answer 1

Hint: In this question we will first prove two triangles congruent with the help of given conditions in the question then with the help of properties came from that proof we will prove OAB triangle as equilateral triangle and finally we will apply angle sum property of triangle and quadrilateral for finding angles asked in the question.

Complete step-by-step answer:
Construction: - First of all we will join points O and B to form side OB, points O and C to form side OC and points A and F to form side AE

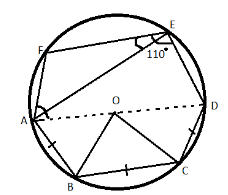
Now in and
$AB = BC$ (Given in question)
$OB = OB$ (Common sides)
$OA = OB$ (Because both are radius of circle)
Therefore by SSS (side side side) test of a triangle.
$ \Rightarrow OA = BC$
But we know that $AB = BC$ therefore $OA = AB = BC$
Hence is an equilateral triangle.
As we know all angles of equilateral triangle is 60 degree therefore \[\angle OAB = \angle AOB = \angle OBA = {60^ \circ }\]
Now AFED is a cyclic quadrilateral so sum of each pair of opposite angles is 180 degree
$ \Rightarrow \angle FAD + \angle DEF = {180^ \circ }$
$ \Rightarrow \angle FAD + {110^ \circ } = {180^ \circ }$ (Angle DEF is given in the question)
$ \Rightarrow \angle FAD = {70^ \circ }$
Now we have to find \[\angle FAB\]
$ \Rightarrow \angle FAD + \angle OAB = \angle FAB$
$ \Rightarrow {70^ \circ } + {60^ \circ } = \angle FAB$
$ \Rightarrow \angle FAB = {130^ \circ }$
Now $\angle AED = {90^ \circ }$ (Angle in a semi circle)
Therefore $\angle AEF = \angle FED - \angle AED$
$\angle AEF = {110^ \circ } - {90^ \circ }$
$\therefore \angle AEF = {20^ \circ }$

Hence we have found out \[\angle AEF\] and \[\angle FAB\] which are 20 degree and 130 degree.

Note: Students may likely to make mistakes while applying properties of a cyclic quadrilateral so below mentioned some of the properties:-
A cyclic quadrilateral is a type of quadrilateral whose all four vertices must lie on a circle. It is also called an inscribed quadrilateral.
The sum of opposite angles of a cyclic quadrilateral is supplementary i.e. 180 degree.
Sum of all the angles equals to 360 degree.