
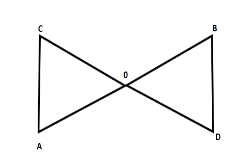
In the given figure AB and CD bisect each other at O.
(i) State the three pairs of equal parts in two triangles AOC and BOD
(ii) Which of the following statements are true?
a) $\vartriangle AOC \cong \vartriangle DOB$
b) $\vartriangle AOC \cong \vartriangle BOD$

Answer
585k+ views
Hint: In the question, $' \cong '$ sign means congruency or congruent. On the basis of similarities between the two triangles they can be called as congruent as per the following criteria:
1. Side Side Side (SSS) – all the three sides of both the triangles are the same.
2. Side Angle Side (SAS) – two sides and the angle between them is same in both the triangles
3. Angle Side Angle (ASA) – two angles and the side between them is same in both the triangles
4. Angle Angle Side (AAS) – two angles and the adjacent side is same in both the triangles
Complete step-by-step answer:
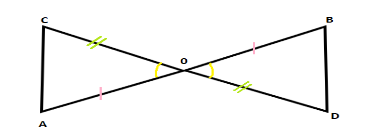
AB and CD bisects each other at O
=> AO = 0B and CO = OD
Because bisecting means dividing into two equal halves.
i) In \[\vartriangle AOC\] and \[\vartriangle BOD\], the three pairs of equal parts are :
CO = O D (Bisected)
$\angle COA = \angle BOD$ (Vertically opposite angles)
AO = 0B (Bisected)
Two sides and the angle between them are same in both the triangles
This shows that $\vartriangle AOC \cong \vartriangle BOD$
ii) The order of writing congruent triangles depend upon the corresponding parts i.e. the order in which they are written should also be the order for their congruency.
This shows that out of the given statements, statement b) $\vartriangle AOC \cong \vartriangle BOD$ is true.
Note: In simple terms if one figure is congruent to another, this means that they can look alike by turning, flipping or sliding. The angles which are vertically opposite in direction are always equal.
AAA (Angle Angle Angle) can also be a congruence criteria but is not used because it is not sufficient to tell whether the two triangles are congruent or not.
1. Side Side Side (SSS) – all the three sides of both the triangles are the same.
2. Side Angle Side (SAS) – two sides and the angle between them is same in both the triangles
3. Angle Side Angle (ASA) – two angles and the side between them is same in both the triangles
4. Angle Angle Side (AAS) – two angles and the adjacent side is same in both the triangles
Complete step-by-step answer:

AB and CD bisects each other at O
=> AO = 0B and CO = OD
Because bisecting means dividing into two equal halves.
i) In \[\vartriangle AOC\] and \[\vartriangle BOD\], the three pairs of equal parts are :
CO = O D (Bisected)
$\angle COA = \angle BOD$ (Vertically opposite angles)
AO = 0B (Bisected)
Two sides and the angle between them are same in both the triangles
This shows that $\vartriangle AOC \cong \vartriangle BOD$
ii) The order of writing congruent triangles depend upon the corresponding parts i.e. the order in which they are written should also be the order for their congruency.
| $\vartriangle AOC \cong \vartriangle DOB$ | $\vartriangle AOC \cong \vartriangle BOD$ |
| AO ≠ DO | AO = BO |
| OC ≠ OB | OC = OD |
This shows that out of the given statements, statement b) $\vartriangle AOC \cong \vartriangle BOD$ is true.
Note: In simple terms if one figure is congruent to another, this means that they can look alike by turning, flipping or sliding. The angles which are vertically opposite in direction are always equal.
AAA (Angle Angle Angle) can also be a congruence criteria but is not used because it is not sufficient to tell whether the two triangles are congruent or not.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




