Question

In the given figure AB and CD are respectively the smallest and largest side of a quadrilateral ABCD. Show that$\angle A > \angle C$ and $\angle B > \angle D$.

Answer 1

Hint: Solve this problem by using the theorem of triangle that is opposite angle of longest side is always greater and angle opposite to the shortest side is always shorter.

Complete Step-by-step Solution
Given:

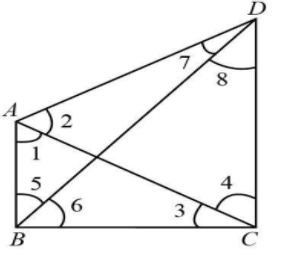
In quadrilateral ABCD, AB and CD are respectively the smallest and largest side of quadrilateral.
From the figure consider$\Delta ABC$, where AB is the shortest side of the triangle. So the angle opposite to the side will be shortest between all angles.
Angle opposite to the side AB is $\angle 3$ and angle opposite to the side BC is $\angle 1$.
$\begin{array}{l}
AB < BC\\
\angle 3 < \angle 1
\end{array}$……....(1)
In$\Delta ADC$, AD is the longest side of the triangle and rest sides are shorter than AD. So the angle opposite to the side will be largest between all angles.
Angle opposite to the side AD is $\angle 4$ and angle opposite to the side CD is $\angle 2$.
$\begin{array}{l}
CD > AD\\
\angle 2 > \angle 4
\end{array}$……..(2)
On adding both the equations (1) and (2), we get the values as,
$\begin{array}{l}
\angle 3 + \angle 4 < \angle 1 + \angle 2\\
\angle C < \angle A\,{\rm{or}}\,\angle A > \angle C
\end{array}$
Now, we are considering the triangles $\Delta ABD$ and $\Delta BCD$.
In triangle $\Delta ABD$, we have,
$\begin{array}{l}
AD > AB\\
\angle 5 > \angle 6
\end{array}$ ……(3)
In triangle $\Delta BCD$, we have,
$\begin{array}{l}
CD > BC\\
\angle 7 > \angle 8
\end{array}$ …...(4)
On adding the equations (3) and (4), we get the values as,
 $\begin{array}{c}
\angle 5 + \angle 7 > \angle 6 + \angle 8\\
\angle B > \angle D
\end{array}$
Therefore, it is proved that $\angle B > \angle D$ and $\angle A > \angle C$.

Note: The important point to solve the problem is that while choosing the other side of triangle make sure the side chosen by you is opposite to that angle which have to be proved in question.