Question

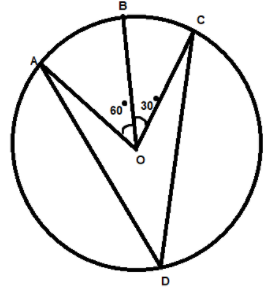
In the given figure , A,B and C are three points on a circle with centre O such that $\angle BOC = {30^ \circ }$ and $\angle AOB = {60^ \circ }$. If D is a point on the circle other than the arc ABC, find $\angle ADC$ ?

Answer 1

Hint:
From the given angles we get the angle subtended by the arc at the centre to be ${90^ \circ }$ and then by using the property that the angle subtended by an arc at the centre is twice the angle subtended by the arc at any other point on the circle we can get the value of $\angle ADC$.

Complete step by step solution:
We are given a circle and A , B and C are the points on the circle
And its given that $\angle BOC = {30^ \circ }$ and $\angle AOB = {60^ \circ }$

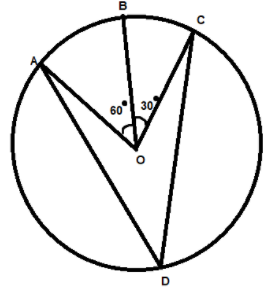
From the diagram we can get that
$
   \Rightarrow \angle AOC = \angle AOB + \angle BOC \\
   \Rightarrow \angle AOC = {60^ \circ } + {30^ \circ } \\
   \Rightarrow \angle AOC = {90^ \circ } \\
 $
We can see that $\angle AOC$ is the angle subtended at the centre by the arc ABC
Now D is the point on the circle other than the arc ABC
Hence we know that the angle subtended by an arc at the centre is twice the angle subtended by the arc at any other point on the circle
Therefore we get
$
   \Rightarrow \angle AOC = 2 \times \angle ADC \\
   \Rightarrow {90^ \circ } = 2 \times \angle ADC \\
   \Rightarrow \dfrac{{{{90}^ \circ }}}{2} = \angle ADC \\
   \Rightarrow {45^ \circ } = \angle ADC \\
 $

Hence we get the value of $\angle ADC$ as ${45}^{\circ}$.

Note:
1) Angles in the same segment of a circle are equal.
2) The angle at the centre of a circle is twice the angle at the circumference subtended by the same arc.
3) The angle subtended by a diameter at the circumference is equal to a right angle.
4) The opposite angles of a quadrilateral inscribed in a circle sum to two right angles.