Question

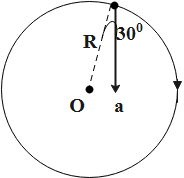
In the given figure \[a=15\dfrac{m}{{{s}^{2}}}\] represents the total acceleration of particle moving in the clockwise direction in a circle of radius R = 2.5 m at a given instant of time. If the square of the speed of the particle is \[\dfrac{75\sqrt{3}}{n}\dfrac{{{m}^{2}}}{{{s}^{2}}}\]. Then write the value of n.

Answer 1

Hint: This is a direct question. Using the centripetal acceleration formula, we can solve this problem, as we can obtain the expression for the velocity, as the product of the radius of the circle and the total acceleration of the particle. As these values are given, so, substituting these values, we will find the value of n.

Formula used:
\[{{a}_{C}}=\dfrac{{{V}^{2}}}{R}\]

Complete step by step answer:
The formula that relates the centripetal acceleration, the velocity of the particle and the radius of the circle is given as follows.
\[{{a}_{C}}=\dfrac{{{V}^{2}}}{R}\]
From the data, we have the data as follows.
The total acceleration of the particle moving in the clockwise direction is, \[a=15\dfrac{m}{{{s}^{2}}}\]
The radius of the circle is, R = 2.5 m
The square of the speed of the particle is,\[{{v}^{2}}=\dfrac{75\sqrt{3}}{n}\dfrac{{{m}^{2}}}{{{s}^{2}}}\].
Consider the diagram while going through the calculation.

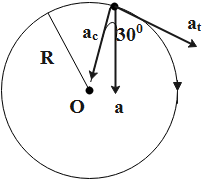
The above figure represents the centripetal acceleration and the tangential acceleration, the components of the acceleration of the particle.
The centripetal acceleration of the particle is given as follows.
\[{{a}_{C}}=a\cos 30{}^\circ \]
Substitute the given values in the above equation.
\[\dfrac{{{V}^{2}}}{R}=a\cos 30{}^\circ \]

\[\dfrac{{{V}^{2}}}{2.5}=15\cos 30{}^\circ \]

Continue the further calculation.
\[\begin{align}
  & {{v}^{2}}=2.5\times 15\cos 30{}^\circ \\
 & {{v}^{2}}=\dfrac{2.5\times 15\times \sqrt{3}}{2} \\
 & \Rightarrow {{v}^{2}}=\dfrac{75\sqrt{3}}{4} \\
\end{align}\]

Compare this obtained value of the square of the speed of the particle with the given value of the square of the speed of the particle. So, we get,

\[\dfrac{75\sqrt{3}}{n}=\dfrac{75\sqrt{3}}{4}\]

Cancel out the common terms.
\[n=4\]

Therefore, the value of the n is 4.

Note:
The units of the parameters should be taken care of. The main point to remember while solving such problems is the components of the acceleration of the particle, that is, the centripetal acceleration and the tangential acceleration. The formula that relates the centripetal acceleration with the velocity of the particle should also be known. In this case, the value of n is asked. Even, they can directly ask for the value of the velocity of the particle.