Question

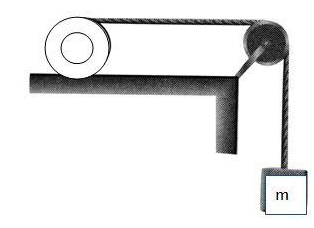
In the given figure a ring of mass m is kept on a horizontal surface while a body of equal mass m is attached through a string, which is wounded on the ring, When the system is released, the ring rolls without slipping Consider the following statement and choose the correct option


(i) acceleration of the centre of mass of ring is 2g​/3
(ii) acceleration of hanging particle is 4g​/3
(iii) frictional force (on the ring) acts in forward direction
(iv) frictional force (on the ring) acts in backward direction

Answer 1

Hint:-analyze the figure and draw free body diagram( diagram used to show the relative magnitude and direction of all forces acting upon an object ) for block and ring then write equation
We have given here a block of mass m is attached through a string which is bounded on the ring

Formula used
Force=mass x acceleration
Moment of inertia for ring=mR2

Complete step by step solution

Free body diagram for Block
\[mg - T = m(2a)\]...........................(1)

          

here weight of block=mg ,T=tension in upward direction
2a= acceleration

free body diagram for Ring in translational motion

\[\;T + f = ma\] \[T + f = ma\]........................(2)
Where T = tension , f= friction
 Now free body diagram for ring in rotational ,motion
\[TR - fR = I\;\alpha \]
 where I= moment of inertia = mR2 for ring
 F= friction ,R= radius of ring
 So , \[TR - fR = m{R^2}\]
 \[T - f{\text{ }} = {\text{ }}mR\alpha \]
Since \[f = 0\] \[R\alpha = a\]
 \[T - f = ma\] (3)
Now from (1) and (2)
\[2T = ma\] (4)
 And from (1) and (4)
 \[Mg = 3ma\]
So, \[a = g/3\]
Or putting in (4) we get,
 \[T{\text{ }} = {\text{ }}mg/3\]
From this we can say option (1) and (ii) is incorrect
 Now for friction we need to substitute the above value
 \[f = T{\text{ }}-ma\]
therefore\[f = 0\]

Therefore option (D) is correct

Note:-here option C and D are incorrect because there is no friction so friction force in the ring is not possible neither in upward nor in downward. In this type of question when a ring is moving then we need to analyze both the condition rotational as well as translational.