Question

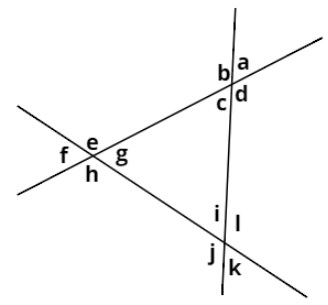
In the given figure ${\text{a, b, c, d,}}...$ are measures of respective angles as shown. If $g = {90^ \circ }$, what is ${\text{a + k}}$?

A. 135
B. 45
C. 90
D. 60

Answer 1

Hint: Consider the triangle with angles ${\text{g, i and c}}$ in the figure. Use the property that the sum of angles in a triangle is ${180^ \circ }$. And then apply the property of opposite angles.

Complete step by step answer:
We know that the sum of angles in a triangle is ${180^ \circ }$. So from the figure, in triangle with angles ${\text{g, i and c}}$, we have:
$ \Rightarrow g + i + c = {180^ \circ }$
According to the question $g = {90^ \circ }$. Putting its value above, we’ll get:
$
   \Rightarrow {90^ \circ } + i + c = {180^ \circ } \\
   \Rightarrow i + c = {90^ \circ } .....(i) \\
$
Again from figure, angles $i$ and $k$ are opposite angles. Thus they will be equal in measure.
$ \Rightarrow i = k$
Same is the case with $a$ and $c$ also. So, we have:
 $ \Rightarrow c = a$
Putting $i = k$ and $c = a$ in equation $(i)$, we’ll get:
$ \Rightarrow k + a = {90^ \circ }$

Hence the value of ${\text{a + k}}$ is ${90^ \circ }$.

Note: The sum of the angles in an n sided polygon is given by the formula:
$ \Rightarrow $ Sum of angles $ = \left( {n - 2} \right) \times {180^ \circ }$.
If it is a triangle then $n = 3$ and the sum of angles is ${180^ \circ }$.