Question

In the given figure A, B, C and D are concyclic points. The value of x is

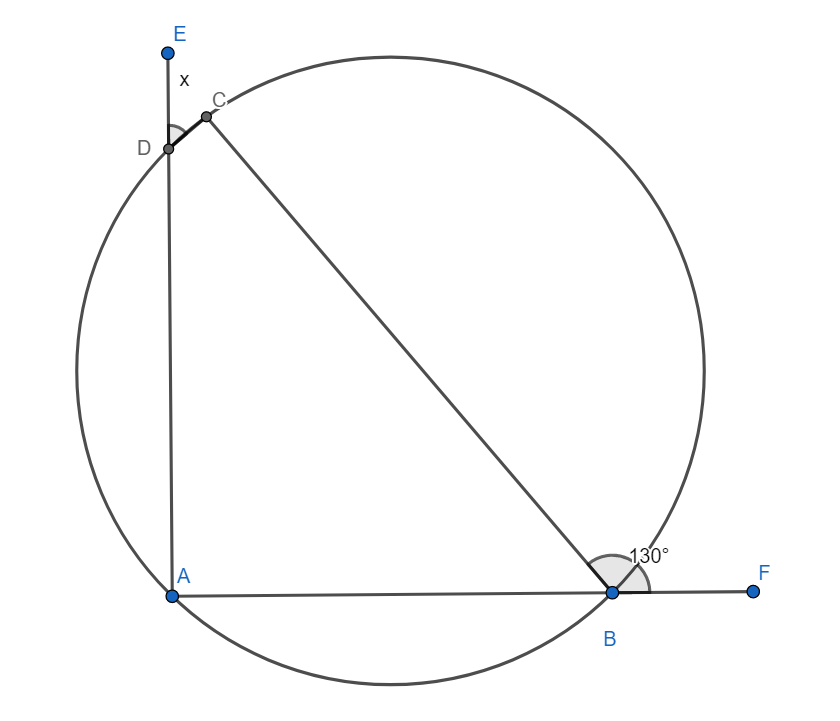
[a] $50{}^\circ $
[b] $60{}^\circ $
[c] $70{}^\circ $
[d] $90{}^\circ $

Answer 1

Hint: Find the measure of $\angle CBA$ using the fact that the angles CBA and CBF form a linear pair. Using the fact that the sum of opposite angles of a cyclic quadrilateral, find the measure of angle CDA. Finally, using the fact that the angles CDA and CDE from a linear pair find the measure of angle ECD. Hence find the value of x. Alternatively, use the fact that the exterior angle of a cyclic quadrilateral is equal to the interior opposite angle and hence find the measure of x.

Complete step-by-step answer:

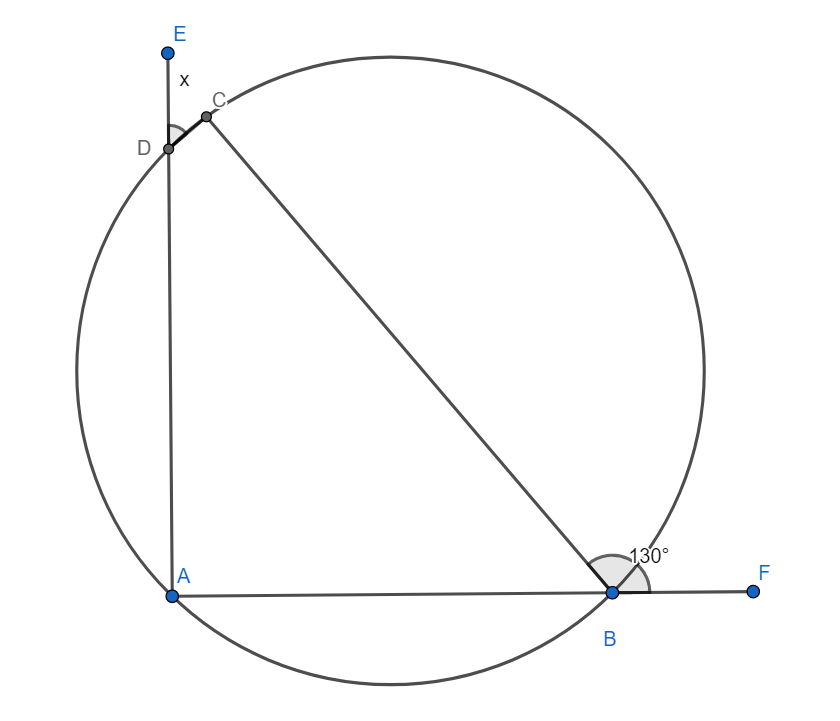
Given: ABCD is a cyclic quadrilateral. Side AB is extended to point F, and AD is extended to point E. The measure of angle FBC is $130{}^\circ $ , and the measure of angle ECD is x.
To determine: The value of x.
Since ABF are collinear, we have angles CBA and CBF form a linear pair
Hence, we have
$\angle CBF+\angle CBA=180{}^\circ $
Substituting the value of $\angle CBF$, we get
$130{}^\circ +\angle CBA=180{}^\circ $
Subtracting 130 on both sides, we get
$\angle CBA=50{}^\circ $
Now, we know that the sum of measures of opposite angles of a cyclic quadrilateral is $180{}^\circ $. Since angles CDA and CBA are opposite angles of the cyclic quadrilateral ABCD, we have
$\angle CDA+\angle CBA=180{}^\circ $
Substituting the value of $\angle CBA,$ we get
$\angle CDA+50{}^\circ =180{}^\circ $
Subtracting 50 from both sides of the equation, we get
$\angle CDA=130{}^\circ $
Now, since A,D and E are collinear, we have the angels EDC and CDA form a linear pair
Hence, we have
$\angle EDC+\angle CDA=180{}^\circ $
Substituting the value of $\angle EDC$ and $\angle CDA$, we get
$x+130{}^\circ =180{}^\circ $
Subtracting 130 on both sides, we get
$x=50{}^\circ $
Hence the value of x is $50{}^\circ $
Hence option [a] is correct.

Note: Alternative solution:
We know that the exterior angle of the cyclic quadrilateral is equal to the interior opposite angle.
Since $\angle EDC$ is an exterior angle of the cyclic quadrilateral ABCD and $\angle CBA$ is the corresponding interior opposite angle, we have
$x=\angle CBA=50{}^\circ $
Hence, the value of x is $50{}^\circ $