Question

In the given figure :

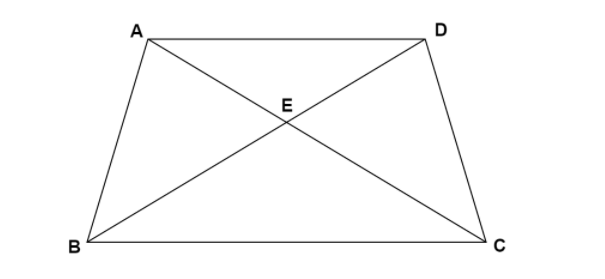
1.What is \[AE + EC\] ?
2.What is \[AC - EC\] ?
3.What is \[BD - BE\] ?
4.What is \[BD - DE\] ?

Answer 1

Hint: In the given question , we have a quadrilateral \[ABCD\] whose diagonals intersect at \[E\] . Now , in the question we have to add and subtract the segments of the given diagonals . As from the figure we have \[AC = AE + EC\] and \[BD = BE + ED\] , now using these conditions we will solve the question .

Complete step-by-step answer:
The given figure is a quadrilateral \[ABCD\] , in which \[AC\] and \[BD\] are the diagonals of this quadrilateral and \[E\] is the point of intersection of the diagonals .
Now , solving the first case we get :
\[AE + EC = ?\]
Using the diagonals conditions we have ,
\[AC = AE + EC\] .
Now , solving the second case we have ,
\[AC - EC = ?\]
Using the diagonals conditions we have ,
\[AC = AE + EC\]
Now , shifting \[EC\] to LHS we have ,
\[AC - EC = AE\] .
Now solving the third case we have ,
\[BD - BE = ?\]
Using the diagonals conditions we have ,
\[BD = BE + ED\]
Shifting \[BE\] to LHS we have ,
\[BD - BE = DE\] .
Now , solving the fourth case we have ,
\[BD - DE = ?\]
Using the diagonals conditions we have ,
\[BD = BE + ED\]
Shifting \[DE\] to LHS we have ,
\[BD - ED = BE\] .
Now we can write \[DE = ED\] as line segment points . Therefore , we have
\[BD - DE = BE\] .
Therefore , we have
1.\[AE + EC = AC\]
2.\[AC - EC = AE\]
3.\[BD - BE = DE\]
4.\[BD - DE = BE\]

Note: If the diagonal or any other sides are intersected by any other diagonal or line segment , then that diagonal or line is divided into several parts or segments and then we can write the whole line into parts , for example we have \[AC\] ( from the figure ) it can be written as \[AE + EC\] , as \[E\] is the intersecting point .