Question

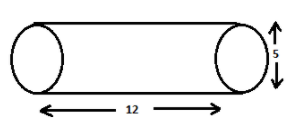
In the given closed cylinder, the stick of maximum length_ _ _ _ _ _ _ _can be kept inside it.
     

$
  A.10 \\
  B.12 \\
  C.13 \\
  D.17 \\
$

Answer 1

Hint: In this question we have to work out the largest rod which can be kept in a solid closed cylinder. To solve this question, construction diameter in any one plane surface. We know base cured surface & drawn diameter will subtend right angled with each other to work out the hypotenuse. Its hypotenuse is the diagonal of that cylinder and is the longest length of this figure.

Complete step-by-step answer:
     

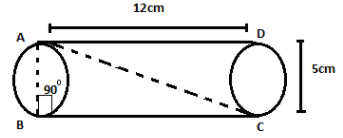
Join $AB$ diameter of circle passing through $A$, $B$
Given –
\[AB = CD\]\[ = \]diameter\[ = 5cm\]
\[BC = AD = 12cm\]
\[\therefore \]In \[\Delta ABC\]-
\[
  {\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2} \\
   = {\left( 5 \right)^2} + {\left( {12} \right)^2} \\
   = 25 + 144 \\
   = 169 \\
\]
\[\therefore AC = \sqrt {169} = 13cm\]
\[\therefore \]Stick with maximum length \[13cm\] can be kept.

Note: In lower classes, we have learnt about many solid figures, and their properties. We also came across one of their parts called diagonal. In any solid figure such as rectangle, square, cube, cuboid, rhombus etc. the longest sticks which can be kept are their diagonals. The solid figures make right angled with their two adjacent sides. So, diagonals become their hypotenuse such as, in rectangle \[ABCD\], \[\]\[AB\] & \[BC\] make \[{90^0}\], So, \[AC\] is hypotenuse as well as diagonal for \[ABCD\]. In every right-angled, triangle, hypotenuse has maximum length. So, taking out the value of hypotenuse or diagonal, we got the longest stick kept in any figure. In this way this type of question is solved.