Question

In the given circuit, the direction of current in the MN wire is:

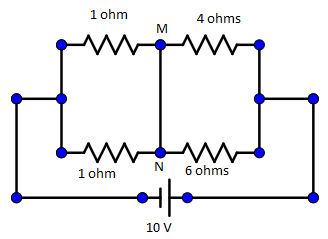
(A) no current
(B) M to N
(C) any direction
(D) N to M

Answer 1

Hint
First we have to determine the equivalent resistance of the four resistors. Then by using the ohm’s law, the current in the circuit is determined by using the equivalent resistance and the voltage given in the question. Then the current through the two parallel resistors can be determined, by the two current values from the two parallel resistors the direction can be determined.
Resistors in parallel is given by,
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
The current through the resistor is given by,
$\Rightarrow i = \dfrac{V}{R}$
Where, $i$ is the current, $V$ is the voltage and $R$ is the resistance.

Complete step by step answer
The first two resistance are in parallel, by using the resistance in parallel formula, then
$\Rightarrow \dfrac{1}{{{R_{{p_1}}}}} = \dfrac{1}{1} + \dfrac{1}{1}$
Where, ${R_{{p_1}}}$ is the first pair of resistance in parallel.
By adding the above equation, then
$\Rightarrow \dfrac{1}{{{R_{{p_1}}}}} = \dfrac{2}{1}$
By taking reciprocal on both sides, then
$\Rightarrow {R_{{p_1}}} = \dfrac{1}{2}$
On dividing the above equation, then
$\Rightarrow {R_{{p_1}}} = 0.5\,\Omega $
The second two resistance are in parallel, by using the resistance in parallel formula, then
$\Rightarrow \dfrac{1}{{{R_{{p_2}}}}} = \dfrac{1}{4} + \dfrac{1}{6}$
Where, ${R_{{p_2}}}$ is the second pair of resistance in parallel.
By cross multiplying the above equation, then
$\Rightarrow \dfrac{1}{{{R_{{p_2}}}}} = \dfrac{{6 + 4}}{{4 \times 6}}$
On further simplification, then the above equation is written as,
$\Rightarrow \dfrac{1}{{{R_{{p_2}}}}} = \dfrac{{10}}{{24}}$
By taking reciprocal on both sides, then
$\Rightarrow {R_{{p_2}}} = \dfrac{{24}}{{10}}$
On dividing the above equation, then
$\Rightarrow {R_{{p_2}}} = 2.4\,\Omega $
Now, the total resistance is the sum of the individual resistance, then
$\Rightarrow R = {R_{{p_1}}} + {R_{{p_2}}}$
On substituting the values of the resistance, then
$\Rightarrow R = 0.5 + 2.4$
By adding the above equation, then
$\Rightarrow R = 2.9\,\Omega $
Now, the current in the circuit is given by,
$\Rightarrow i = \dfrac{V}{R}$
On substituting the voltage and resistance, then
$\Rightarrow i = \dfrac{{10}}{{2.9}}$
On dividing the above equation, then
$\Rightarrow i = 3.44\,A$
The current through the first pair of parallel resistance is,
$\Rightarrow {i_1} = \dfrac{V}{{{R_{{p_1}}}}}$
On substituting the voltage and resistance in the above equation, then
$\Rightarrow {i_1} = \dfrac{{10}}{{0.5}}$
On dividing the terms, then
$\Rightarrow {i_1} = 20\,A$
The current through the second pair of parallel resistance is,
$\Rightarrow {i_2} = \dfrac{V}{{{R_{{p_2}}}}}$
On substituting the voltage and resistance in the above equation, then
$\Rightarrow {i_2} = \dfrac{{10}}{{2.4}}$
On dividing the terms, then
$\Rightarrow {i_2} = 4.16\,A$
By the current ${i_1}$ and ${i_2}$, the direction of the will be M to N.
Hence, the option (B) is the correct answer.

Note
The current in the circuit and the resistance in the same circuit is always inversely proportional to each other under the constant voltage. The first pair of the parallel resistance is the low resistance but the first pair having the high current, like that the second pair of parallel resistance have high resistance so it has less current.