Question

In the given circuit, the current \[I\] equals to:

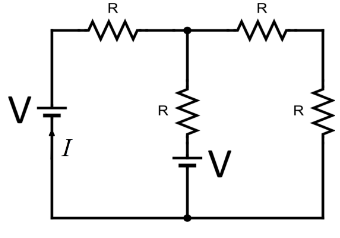
A. \[\dfrac{V}{{5R}}\]
B. \[\dfrac{V}{{4R}}\]
C. \[\dfrac{{2V}}{{5R}}\]
D. \[0\]

Answer 1

Hint: To solve this problem, use Kirchhoff’s voltage law for both the loops and find the current through the circuit solving the equations. Kirchhoff’s voltage law states that in any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop. Mathematical expression of the Kirchhoff’s voltage law can be given as, \[\sum {{V_j}} = \sum {{I_i}{R_i}} \] where \[\sum {{V_j}} \] is the algebraic sum of all the voltage sources and \[\sum {{I_i}{R_i}} \] is the algebraic sum of all the voltage drops across elements.

Complete step by step answer:
In the given circuit let’s take the first loop as loop-I and another as loop –II . Let’s assume the current through the loop-I is \[I\]and current through loop –II is \[{I_1}\].

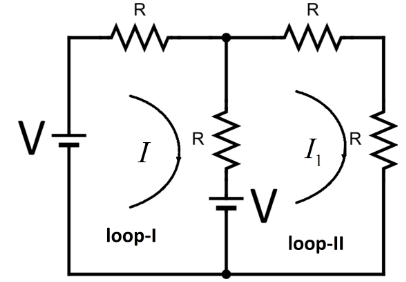
So, applying KVL in the first loop we can get,( loop-I)
\[IR + (I - {I_1})R = V - V\]
\[\Rightarrow IR + (I - {I_1})R = 0\]
Further simplifying we get,
\[2IR = {I_1}R\]
\[\Rightarrow {I_1} = 2I\]..........................[Since, resistance \[R\] is not zero]
Now, applying KVL in the second loop we can get,( loop –II)
\[({I_1} - I)R + {I_1}R + {I_1}R = V\]
\[\Rightarrow ({I_1} - I)R + 2{I_1}R = V\]
Putting the value of \[{I_1}\] from previous equation we get,
\[(2I - I)R + 2 \cdot 2I \cdot R = V\]
\[\Rightarrow IR + 4IR = V\]
\[\Rightarrow 5IR = V\]
\[\therefore I = \dfrac{V}{{5R}}\]
Hence, the current through the first loop will be equal to \[\dfrac{V}{{5R}}\]. Now, we can see that this is the same current as the circuit current. So, the current \[I\] is equal to \[\dfrac{V}{{5R}}\].

Hence, the correct answer is option A.

Note: The sign convention for the voltage source is: when a voltage source is traversed from positive terminal to negative terminal then voltage of the source is taken as negative and when a voltage source is traversed from negative terminal to positive terminal then voltage of the source is taken as positive. Voltage drop across an element for a loop current is negative when the current is flowing in the opposite direction of the loop traversed and it is taken positive when the current is flowing in the same direction of the loop traversed.