Question

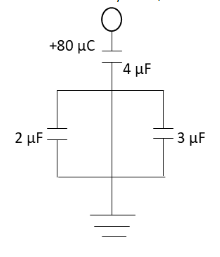
In the given circuit, a charge of \[80\,\mu {\text{C}}\] is given to the upper plate of the \[4\,\mu {\text{F}}\] capacitor. Then in the steady state, the charge on the upper plate of the \[3\,\mu {\text{F}}\] capacitor is:

A. \[ + 32\,\mu {\text{C}}\]
B. \[ + 40\mu {\text{C}}\]
C. \[ + 48\,\mu {\text{C}}\]
D. \[ + 80\,\mu {\text{C}}\]

Answer 1

Hint: Use the formula for the charge stored on the plates of the capacitor. The total charge given the upper plate of the capacitor is equal to the sum of the charges stored on the plates of the remaining two capacitors. Since the two capacitors are in parallel, the potential across the plates of these two capacitors should be equal.

Formula used:
The charge \[q\] stored on the plates of the capacitor is
\[q = CV\] …… (1)
Here, \[C\] is the capacitance and \[V\] is the potential difference.

Complete step by step answer:
We have given that a charge of \[80\,\mu {\text{C}}\] is given to the upper plate of the \[4\,\mu {\text{F}}\] capacitor.
\[q = 80\,\mu {\text{C}}\]

Let A, B and C be the capacitors with capacitances \[4\,\mu {\text{F}}\], \[2\,\mu {\text{F}}\] and \[3\,\mu {\text{F}}\] respectively. Let \[{q_A}\], \[{q_B}\] and \[{q_C}\] be the charges stored and \[{V_A}\], \[{V_B}\] and \[{V_C}\] be the potentials across the plates of capacitors \[4\,\mu {\text{F}}\], \[2\,\mu {\text{F}}\] and \[3\,\mu {\text{F}}\] respectively.

The charge \[80\,\mu {\text{C}}\] given to the upper plate of the capacitor A will be divided and passed to the two capacitors B and C. Hence, the total charge stored on the plates of the capacitors B and C is \[80\,\mu {\text{C}}\].
\[{q_A} + {q_B} = 80\,\mu {\text{C}}\]

Rewrite equation (1) for the potential across the plates of capacitor B.
\[{V_B} = \dfrac{{{q_B}}}{{{C_B}}}\]
Here, \[{C_B}\] is the capacitance across the capacitor B.

Rewrite equation (1) for the potential across the plates of capacitor C.
\[{V_C} = \dfrac{{{q_C}}}{{{C_C}}}\]
Here, \[{C_C}\] is the capacitance across the capacitor C.

Since the capacitors B and C are connected in parallel, the potential across the plates of the B and C must be the same.
\[{V_B} = {V_C}\]

Substitute \[\dfrac{{{q_B}}}{{{C_B}}}\] for \[{V_B}\] and \[\dfrac{{{q_C}}}{{{C_C}}}\] for \[{V_C}\] in the above equation.
\[\dfrac{{{q_B}}}{{{C_B}}} = \dfrac{{{q_C}}}{{{C_C}}}\]

Substitute \[80\,\mu {\text{C}} - {q_C}\] for \[{q_B}\] in the above equation.
\[\dfrac{{80\,\mu {\text{C}} - {q_C}}}{{{C_B}}} = \dfrac{{{q_C}}}{{{C_C}}}\]

Substitute \[2\,\mu {\text{F}}\] for \[{C_B}\] and \[3\,\mu {\text{F}}\] for \[{C_C}\] in the above equation.
\[\dfrac{{80\,\mu {\text{C}} - {q_C}}}{{2\,\mu {\text{F}}}} = \dfrac{{{q_C}}}{{3\,\mu {\text{F}}}}\]
\[ \Rightarrow 240\,\mu {\text{C}} - 3{q_C} = 2{q_C}\]
\[ \Rightarrow {\text{5}}{q_C} = 240\,\mu {\text{C}}\]
\[ \Rightarrow {q_C} = \dfrac{{240\,\mu {\text{C}}}}{5}\]
\[ \therefore {q_C} = 48\,\mu {\text{C}}\]
From the circuit diagram, we can see that the lower plate of the capacitor C is connected to the ground. Hence, the charge on the upper plate of the capacitor C should be positive.

Therefore, the charge on the upper plate of the \[3\,\mu {\text{F}}\] capacitor is \[ + 48\,\mu {\text{C}}\].

Hence, the correct option is C.

Note: There is no need to convert the units of the capacitance and charge on the capacitors in the SI system of units. The final answer of the required charge on the capacitor is also in micro coulomb. The students should not forget to use that the potential on the two capacitors connected in parallel is equal.