Question

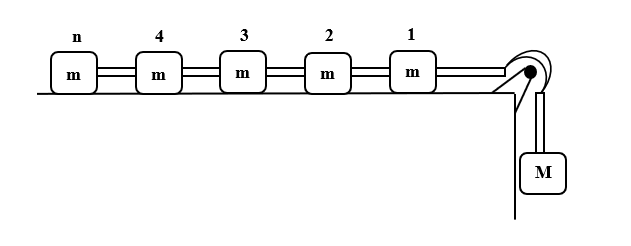
In the given arrangement, n number of equal masses are connected by strings of negligible masses. The tension in the string connected to ${n}^{th}$ mass is:

$A. \dfrac {mMg}{nm + M}$
$B. \dfrac {mMg}{nmM}$
$C. mg$
$D. nmg$

Answer 1

Hint: To solve this question, first find the tension in the string connected to mass M. Then, find the tension in the string connected to n number of equal masses. Equate these two equations. Then, rearrange these equations such that you get the acceleration of these masses. Now, obtain the equation for tension in the string connected to ${n}^{th}$ mass. Substitute the expression for acceleration which you obtained in earlier steps. This will give the tension in the string connected to ${n}^{th}$ mass.

Complete step-by-step answer:
Tension in the string connected to mass M is given by,
$Mg-T= Ma$
$\Rightarrow T= Mg-Ma$ …(1)
Tension in the string connected to n number of equal masses is given by,
$T= nma$ …(2)
Comparing equation. (1) and (2) we get.
$Mg-Ma= nma$
$\Rightarrow Mg= nma+Ma$
$\Rightarrow Mg= a\left(nm+M \right)$
$\Rightarrow a= \dfrac {Mg}{nm+M}$ …(3)
Now, the tension in the string connected to ${n}^{th}$ mass will be given by,
${T}_{n}=ma$
Substituting equation. (3) in above equation we get,
${T}_{n}= \dfrac {mMg}{nm+M}$
Thus, the tension in the string connected to ${n}^{th}$ mass is $\dfrac {mMg}{nm+M}$.
So, the correct answer is option A i.e. $\dfrac {mMg}{nm+M}$.

So, the correct answer is “Option A”.

Note: Students usually get confused between stress and tension. They should remember that the tension is the force acting along the length when an object is pulled from both sides. Whereas stress the effect of force acting on the object. The tension is one of the forces which is produced when mass is attached to a string under gravitational force. S.I unit of tension is the same as that of force which is Newton denoted by N.