Question

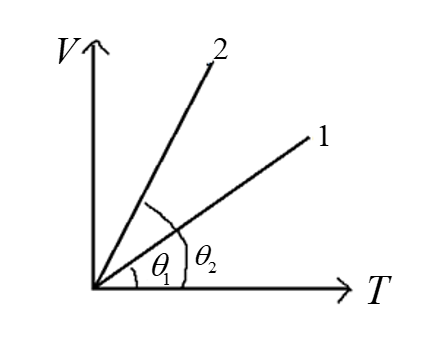
In the following V-T diagram, what is the relation between ${P_1}$ and ${P_2}$.

A) ${P_1} = {P_2}$
B) ${P_2} > {P_1}$
C) ${P_2} < {P_1}$
D) Cannot be predicted.

Answer 1

Hint: A gas which obeys Boyle’s law and Charles’s law strictly at all temperature and pressure is called a perfect or an ideal gas. When heat is supplied to gas at constant pressure, it is used to increase the temperature of the gas and in doing work due to expansion at constant pressure.

Complete step by step answer:
According to Charles’s law at constant pressure, it states that the volume of a given mass of a gas is directly proportional to its temperature.
That is,$V \propto T$ at constant pressure.
$ \Rightarrow \dfrac{V}{T} = {\text{constant}}$ ……………..(1)
Boyle’s law states that the volume of a given mass of a gas is inversely proportional to its pressure $P$ at a constant temperature.
$V \propto \dfrac{1}{P}$ At, constant T.
$ \Rightarrow PV = {\text{constant}}$ ………………….(2)
Combining equation (1) and (2) we get,
$\dfrac{{PV}}{T} = {\text{constant}}$
$\dfrac{{PV}}{T} = R$
For $n$ number of moles, we can write this as,
$PV = nRT$
Where, $R$ is the universal gas constant and $n$ is the number of moles in the sample of a gas.
From the given figure, we have a \[V - T\] diagram for two different pressures.
Slope of the graph is given by,
Slope$ = \dfrac{{y - axis}}{{x - axis}}$
$slope = \dfrac{{\Delta V}}{{\Delta T}}$ ………………..(3)
Now consider ideal gas equation, $PV = nRT$
Rearranging the above equation, we get
$\dfrac{V}{T} = \dfrac{{nR}}{P}$
From equation (3) we can write it as,
$slope = \dfrac{{nR}}{P}$
Here $n$ and $R$ are constants.
Therefore, $slope \propto \dfrac{1}{P}$
The slope of the V-T graph is inversely proportional to the pressure.
For $P_1$, ${(slope)_1} \propto \dfrac{1}{{{P_1}}}$
Here, the slope is less thus the value of ${P_1}$ is more.
 Similarly, for ${P_2}$, ${(slope)_2} \propto \dfrac{1}{{{P_2}}}$
Here, the slope is more thus, ${P_2}$ is less.
Now analyze the result we get, ${P_2}$ is less than ${P_1}$.
$ \Rightarrow {P_2} < {P_1}$

$\therefore $ The correct option is (C).

Note:
Isobaric process: The process in which a system undergoes a change in volume and temperature at constant pressure by the exchange of heat energy with the surroundings is called the isobaric process.
Isochoric process: The process in which a system undergoes a change in pressure and temperature at constant volume by the exchange of heat energy with the surrounding is called the isochoric process.
The universal gas constant is the constant for one mole of a gas. It is the same for all gases, since, at the same temperature and pressure, one mole of any gas occupies the same volume.
For an ideal gas internal energy of a gas depends only on temperature.