Question

In the following figure, two isotropic point sources \[{S_1}\]and \[{S_2}\]emit light in phase at wavelength \[\lambda \]and at the same amplitude. The sources are separated by distance \[2d = 6.00\lambda \]. They lie on an axis that is parallel to an x axis, which runs along a viewing screen at distance \[D = 20.0\lambda \]. The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point P on the screen, at position \[{x_P}\]. What multiple of \[\lambda \] gives the maximum phase difference?

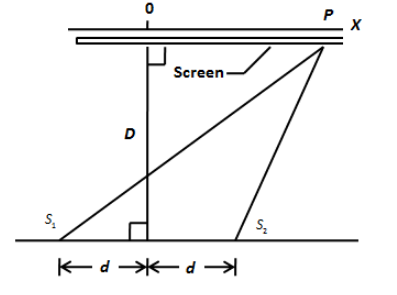
Answer 1

Hint: The phase difference between the rays \[{S_1}P\] and \[{S_2}P\] is \[{S_1}P - {S_2}P\]. Draw the perpendicular lines from \[{S_1}\] and \[{S_2}\] on the screen and use the geometry of the triangles formed by these lines to determine the distance of \[{S_1}P\] and \[{S_2}P\]. Assume \[d \ll D\].

Complete step by step answer:
We have to determine the phase difference between the rays reaching at point P. To do so, we have to redraw the above figure as,

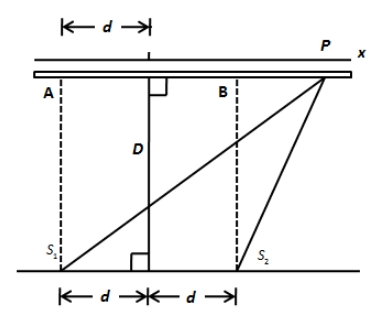
We can see the phase difference between the rays \[{S_1}P\] and \[{S_2}P\] is \[{S_1}P - {S_2}P\]. Let’s use Pythagoras theorem to determine the distance \[{S_1}P\]. In triangle \[{S_1}AP\], using Pythagoras theorem, we can write,
\[{\left( {{S_1}P} \right)^2} = {D^2} + {\left( {x + d} \right)^2}\]
\[ \Rightarrow {\left( {{S_1}P} \right)^2} = {D^2} + {x^2} + 2xd + {d^2}\] …… (1)

In triangle \[{S_2}BP\], using Pythagoras theorem, we can write,
\[{\left( {{S_2}P} \right)^2} = {D^2} + {\left( {x - d} \right)^2}\]
\[ \Rightarrow {\left( {{S_2}P} \right)^2} = {D^2} + {x^2} - 2xd + {d^2}\] …… (2)
Subtracting equation (2) from equation (1), we get,
\[{\left( {{S_1}P} \right)^2} - {\left( {{S_2}P} \right)^2} = 4xd\]
\[ \Rightarrow \left( {{S_1}P - {S_2}P} \right)\left( {{S_1}P + {S_2}P} \right) = 4xd\]
\[ \Rightarrow {S_1}P - {S_2}P = \dfrac{{4xd}}{{{S_1}P + {S_2}P}}\]
If we assume, \[d \ll D\], then we can write, \[{S_1}P + {S_2}P = 2D\]. Therefore, the above equation becomes,
\[{S_1}P - {S_2}P = \dfrac{{4xd}}{{2D}}\]
\[ \Rightarrow {S_1}P - {S_2}P = \dfrac{{2xd}}{D}\]
Substituting \[2d = 6.00\lambda \], \[D = 20.0\lambda \] and \[x = 6.00\lambda \], we get,
\[{S_1}P - {S_2}P = \dfrac{{2\left( 6 \right)\left( 6 \right)}}{{20}}\]
\[ \therefore {S_1}P - {S_2}P = 3.6\]

Therefore, the maximum phase difference is 3.6 times the wavelength.

Note: This question is clearly based on Young’s double slit experiment. Therefore, students must study YDSE to recall the concept of phase difference. In YDSE, if we draw the perpendicular line from \[{S_2}\] on\[{S_1}P\], the distance from \[{S_1}\] to the point where the perpendicular line meets is also the phase difference of the wave.